
如下图,二面角α-l-β的平向角为120°,A∈l,B∈l,AC![]() β,BD
β,BD![]() β,AC⊥l,BD⊥l.若AB=AC=BD=1,则CD长为
β,AC⊥l,BD⊥l.若AB=AC=BD=1,则CD长为

A.![]()
B.![]()
C.2
D.![]()
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源:导学大课堂必修二数学苏教版 苏教版 题型:013
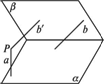
如下图,已知![]() 为异面直线a、b所成的角,α∩β=l,a⊥α,b⊥β,则二面角α-l-β的大小为
为异面直线a、b所成的角,α∩β=l,a⊥α,b⊥β,则二面角α-l-β的大小为
A.![]() 或180°-
或180°-![]()
B.90°-![]()
C.180°-![]()
D.以上都有可能
查看答案和解析>>
科目:高中数学 来源:导学大课堂必修二数学苏教版 苏教版 题型:044
如下图,A、B是二面角α-l-β的棱上两点,在平面α内有一点C,且AC⊥BC,若AC=![]() ,BC=
,BC=![]() ,BC和平面β成30°的角,求二面角α-l-β的大小.
,BC和平面β成30°的角,求二面角α-l-β的大小.

查看答案和解析>>
科目:高中数学 来源: 题型:013
(
珠海二中模拟)已知二面角α—l—β的平面角为θ,PA⊥α,PB⊥β,A、B为垂足,且PA=4,PB=5,点A、B到棱l的距离分别为x、y,当θ变化时,点(x,y)的轨迹是如下图中的[
]
查看答案和解析>>
科目:高中数学 来源: 题型:044
(2006
江苏,19)如下图,在正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足AE∶EB=CF∶FA=CP∶PB=l∶2(如图1).将△AEF沿EF折起到 的位置,使二面角
的位置,使二面角 成直二面角,连结
成直二面角,连结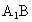 、
、 (如图2).
(如图2).
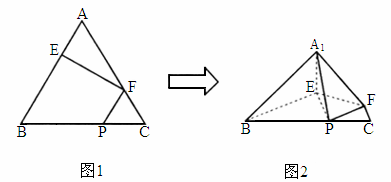
(1)
求证: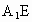 ⊥平面BEP;
⊥平面BEP;
(2)
求直线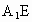 与平面
与平面 所成角的大小;
所成角的大小;
(3)
求二面角 的大小(用反三角函数值表示).
的大小(用反三角函数值表示).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com