
【题目】已知函数 ![]() .
.
(1)求f(x)的最小正周期;
(2)求f(x)在区间 ![]() 上的最大值和最小值.
上的最大值和最小值.
【答案】
(1)解:∵sinxcosx= ![]() sin2x,cos2x=
sin2x,cos2x= ![]() (1+cos2x)
(1+cos2x)
∴f(x)=﹣ ![]() sin(2x+
sin(2x+ ![]() )+6sinxcosx﹣2cos2x+1=﹣sin2x﹣cos2x+3sin2x﹣(1+cos2x)+1
)+6sinxcosx﹣2cos2x+1=﹣sin2x﹣cos2x+3sin2x﹣(1+cos2x)+1
=2sin2x﹣2cos2x=2 ![]() sin(2x﹣
sin(2x﹣ ![]() )
)
因此,f(x)的最小正周期T= ![]() =π;
=π;
(2)解:∵0≤x≤ ![]() ,∴﹣
,∴﹣ ![]() ≤2x﹣
≤2x﹣ ![]() ≤
≤ ![]()
∴当x=0时,sin(2x﹣ ![]() )取得最小值﹣
)取得最小值﹣ ![]() ;当x=
;当x= ![]() 时,sin(2x﹣
时,sin(2x﹣ ![]() )取得最大值1
)取得最大值1
由此可得,f(x)在区间 ![]() 上的最大值为f(
上的最大值为f( ![]() )=2
)=2 ![]() ;最小值为f(0)=﹣2.
;最小值为f(0)=﹣2.
【解析】(1)利用两角和的正弦公式将sin(2x+ ![]() )展开,结合二倍角的正余弦公式化简合并,得f(x)=2sin2x﹣2cos2x,再利用辅助角公式化简得f(x)=2
)展开,结合二倍角的正余弦公式化简合并,得f(x)=2sin2x﹣2cos2x,再利用辅助角公式化简得f(x)=2 ![]() sin(2x﹣
sin(2x﹣ ![]() ),最后利用正弦函数的周期公式即可算出f(x)的最小正周期;(2)根据x∈
),最后利用正弦函数的周期公式即可算出f(x)的最小正周期;(2)根据x∈ ![]() ,得﹣
,得﹣ ![]() ≤2x﹣
≤2x﹣ ![]() ≤
≤ ![]() .再由正弦函数在区间[﹣
.再由正弦函数在区间[﹣ ![]() ,
, ![]() ]上的图象与性质,可得f(x)在区间
]上的图象与性质,可得f(x)在区间 ![]() 上的最大值为与最小值.
上的最大值为与最小值.
【考点精析】利用两角和与差的正弦公式和二倍角的正弦公式对题目进行判断即可得到答案,需要熟知两角和与差的正弦公式:![]() ;二倍角的正弦公式:
;二倍角的正弦公式:![]() .
.


科目:高中数学 来源: 题型:
【题目】为了调查观众对电视剧《风筝》的喜爱程度,某电视台举办了一次现场调查活动.在参加此活动的甲、乙两地大量观众中,各随机抽取了8名观众对该电视剧评分做调查(满分100分),被抽取的观众的评分结果如图所示.

(1)从甲地抽取的8名观众和乙地抽取的8名观众中分别各选取一人,在已知两人中至少一人评分不低于90分的条件下,求乙地被选取的观众评分低于90分的概率。
(2)从甲地抽取出来的8名观众中选取1人,从乙地抽取出来的8名观众中选取2人去参加代表大会,记选取的3人中评分不低于90分的人数为![]() ,求
,求![]() 的分布列与期望。
的分布列与期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列三个命题:
①若一个球的半径缩小到原来的 ![]() ,则其体积缩小到原来的
,则其体积缩小到原来的 ![]() ;
;
②若两组数据的平均数相等,则它们的标准差也相等;
③直线x+y+1=0与圆 ![]() 相切.
相切.
其中真命题的序号是( )
A.①②③
B.①②
C.①③
D.②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的奇函数,且当x<0时,f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图象如图所示,
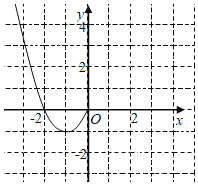
(1)画出函数f(x),x∈R剩余部分的图象,并根据图象写出函数f(x),x∈R的单调区间;(只写答案)
(2)求函数f(x),x∈R的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知首项为 ![]() 的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3 , S5+a5 , S4+a4成等差数列.
的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3 , S5+a5 , S4+a4成等差数列.
(1)求数列{an}的通项公式;
(2)设 ![]() ,求数列{Tn}的最大项的值与最小项的值.
,求数列{Tn}的最大项的值与最小项的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了展示中华汉字的无穷魅力,传递传统文化,提高学习热情,某校开展《中国汉字听写大会》的活动.为响应学校号召,2(9)班组建了兴趣班,根据甲、乙两人近期8次成绩画出茎叶图,如图所示,甲的成绩中有一个数的个位数字模糊,在茎叶图中用![]() 表示.(把频率当作概率).
表示.(把频率当作概率).
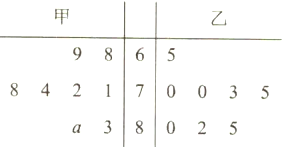
(1)假设![]() ,现要从甲、乙两人中选派一人参加比赛,从统计学的角度,你认为派哪位学生参加比较合适?
,现要从甲、乙两人中选派一人参加比赛,从统计学的角度,你认为派哪位学生参加比较合适?
(2)假设数字![]() 的取值是随机的,求乙的平均分高于甲的平均分的概率.
的取值是随机的,求乙的平均分高于甲的平均分的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com