
【题目】如图,ABCD是边长为2的正方形,ADPM是梯形,AM∥DP且![]() ,
,![]() ,
,![]() 分别为
分别为![]() 的中点.
的中点.
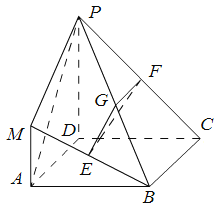
(I)证明:![]() 平面
平面![]() ;
;
(II) 求三棱锥![]() 的体积。
的体积。
【答案】(I)见解析(II) ![]()
【解析】
(I)先根据条件计算出![]() ,得到PD⊥AD, PD⊥CD,
,得到PD⊥AD, PD⊥CD,
则有CD⊥平面ADPM,即得AB⊥平面ADPM,得到AB⊥EG, 又易得AB⊥FG,得证结论.
(II)先证得AD为点P到平面ABM的距离,再根据体积公式求解.
(I)∵![]() 分别为
分别为![]() 的中点,∴BC∥FG, GE∥MP,
的中点,∴BC∥FG, GE∥MP,
∵ABCD是正方形,∴AB⊥BC, ∴AB⊥FG,可得结论.
∵AD=CD=DP=2,![]()
∴![]() ,
,![]()
∴PD⊥AD, PD⊥CD,
∵AD、CP![]() 平面ADPM,AD∩DP=D
平面ADPM,AD∩DP=D
∴CD⊥平面ADPM,
∴AB⊥平面ADPM,
∵MP![]() 平面ADPM,∴AB⊥MP,
平面ADPM,∴AB⊥MP,
∴AB⊥EG,
∵FG、EG![]() 平面EFG,FG∩EG=G
平面EFG,FG∩EG=G
∴![]() 平面
平面![]() ;
;
(II)由(I)可知![]() 平面ABCD ,
平面ABCD ,
∵![]() ,∴
,∴![]() 平面ABCD,
平面ABCD,
∴![]() 又
又![]()
∴ ![]() 平面AMB, ∴AD即为点P到平面ABM的距离,
平面AMB, ∴AD即为点P到平面ABM的距离,
∵![]() ,∴
,∴ ![]() ,
,
∴![]() .
.


 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左
的左![]() 、
、![]() 右焦点分别为,点
右焦点分别为,点![]() 在椭圆上,且满足
在椭圆上,且满足![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设倾斜角为![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,记
两点,记![]() 的面积为
的面积为![]() ,求
,求![]() 取最大值时直线
取最大值时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现采用随机模拟的方法估计某运动员射击4次,至少击中3次的概率;先由计算器给出0到9之间取整数值的随机数,指定0、1、2表示没有击中目标,3、4、5、6、7、8、9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20随机数:![]()
![]()
根据以上数据估计该射击运动员射击4次至少击中3次的概率为( )
A.0.55B.0.6C.0.65D.0.7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,将函数
,将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度,再向下平移
个单位长度,再向下平移![]() 个单位长度后,得到函数
个单位长度后,得到函数![]() 的图象.
的图象.
(1)求函数![]() 的表达式;
的表达式;
(2)当![]() 时,求
时,求![]() 在区间
在区间![]() 上的最大值和最小值;
上的最大值和最小值;
(3)若函数![]() 在
在![]() 上的最小值为
上的最小值为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有![]() 名乒乓球选手进行单循环赛(无和局),比赛结果显示:任意5人中既有1人胜于其余4人,又有1人负于其余4人.则恰胜两场的人数为______个.
名乒乓球选手进行单循环赛(无和局),比赛结果显示:任意5人中既有1人胜于其余4人,又有1人负于其余4人.则恰胜两场的人数为______个.
查看答案和解析>>
科目:高中数学 来源: 题型:
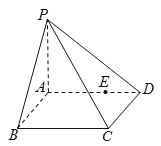
【题目】如图,四棱锥![]() 中,
中,![]() 是矩形,
是矩形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,四棱锥外接球的球心为
,四棱锥外接球的球心为![]() ,点
,点![]() 是棱
是棱![]() 上的一个动点.给出如下命题:①直线
上的一个动点.给出如下命题:①直线![]() 与直线
与直线![]() 是异面直线;②
是异面直线;②![]() 与
与![]() 一定不垂直;③三棱锥
一定不垂直;③三棱锥![]() 的体积为定值;④
的体积为定值;④![]() 的最小值为
的最小值为![]() .其中正确命题的序号是______________.(将你认为正确的命题序号都填上)
.其中正确命题的序号是______________.(将你认为正确的命题序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com