
°æƒø°øŒ™¡ÀΩ‚ ¡‰π´ŒÒ‘±∂‘ø™∑≈…˙”˝∂˛Ã•’˛≤þµƒÃ¨∂»£¨ƒ≥≤ø√≈Àʪ˙µ˜≤È¡À90Œª»˝ ÆÀ͵ΩÀƒ ÆÀ͵ƒπ´ŒÒ‘±£¨µ√µΩ»Áœ¬¡–¡™±Ì£¨“Ú≤ª…˜∂™ ß≤ø∑÷ ˝æð£Æ
£®1£©ÕÍ≥…±Ì∏Ò ˝æð£¨≈–∂œ «∑Ò”–99%“‘…œµƒ∞—Œ’»œŒ™°∞…˙∂˛Ã•“‚‘∏”Ζ‘±”–πÿ°±≤¢Àµ√˜¿Ì”…£ª
£®2£©“—÷™15Œª”–“‚‘∏…˙∂˛Ã•µƒ≈Æ–‘π´ŒÒ‘±÷–”–¡ΩŒª¿¥◊‘ °∏æ¡™£¨∏√≤ø√≈¥ÚÀ„¥”’‚15Œª”–“‚‘∏…˙∂˛Ã•µƒ≈Æ–‘π´ŒÒ‘±÷–Àʪ˙—˚«Î¡ΩŒª¿¥≤Œº”◊˘Ã∏£¨…Ë—˚«Îµƒ2»À÷–¿¥◊‘ °∏æ¡™µƒ»À ˝Œ™X£¨«ÛXµƒ∑÷≤º¡–º∞ ˝—ß∆⁄Õ˚E£®X£©£Æ
ƒ––‘π´ŒÒ‘± | ≈Æ–‘π´ŒÒ‘± | ◊к∆ | |
”–“‚‘∏…˙∂˛Ã• | 15 | 45 | |
ŒÞ“‚‘∏…˙∂˛Ã• | 25 | ||
◊к∆ |
P£®k2°ðk0£© | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
∏Ω£∫ ![]() £Æ
£Æ
°æ¥∞∏°ø
£®1£©Ω‚£∫
ƒ––‘π´ŒÒ‘± | ≈Æ–‘π´ŒÒ‘± | ◊к∆ | |
”–“‚‘∏…˙∂˛Ã• | 30 | 15 | 45 |
ŒÞ“‚‘∏…˙∂˛Ã• | 20 | 25 | 45 |
◊к∆ | 50 | 40 | 90 |
”…”⁄K2= ![]() =4.5£º6.635£¨
=4.5£º6.635£¨
π √ª”–99%“‘…œµƒ∞—Œ’»œŒ™°∞…˙∂˛Ã•“‚‘∏”Ζ‘±”–πÿ°±
£®2£©Ω‚£∫”…“‚ø…µ√£¨“ª√˚ƒ–π´ŒÒ‘±“™…˙∂˛Ã•“‚‘∏µƒ∏≈¬ Œ™ ![]() =
= ![]() £¨ŒÞ“‚‘∏µƒ∏≈¬ Œ™
£¨ŒÞ“‚‘∏µƒ∏≈¬ Œ™ ![]() £¨º« ¬º˛A£∫’‚»˝»À÷–÷¡…Ÿ”–“ª»À“™…˙∂˛Ã•£¨«“∏˜»À“‚‘∏œýª•∂¿¡¢£Æ
£¨º« ¬º˛A£∫’‚»˝»À÷–÷¡…Ÿ”–“ª»À“™…˙∂˛Ã•£¨«“∏˜»À“‚‘∏œýª•∂¿¡¢£Æ
‘ÚP£®A£©=1©ÅP ![]() =1©Å
=1©Å ![]() =
= ![]() £Æ
£Æ
¥£∫’‚»˝»À÷–÷¡…Ÿ”–“ª»À”–“‚‘∏…˙∂˛Ã•µƒ∏≈¬ Œ™ ![]() £Æ
£Æ
Xø…ƒÐµƒ»°÷µŒ™0£¨1£¨2£Æ¿˚”√P£®X=k£©= ![]() £¨ø…µ√P£®X=0£©=
£¨ø…µ√P£®X=0£©= ![]() £¨P£®X=1£©=
£¨P£®X=1£©= ![]() £¨µ√P£®X=2£©=
£¨µ√P£®X=2£©= ![]() £Æ
£Æ
X | 0 | 1 | 2 |
P |
|
|
|
E£®X£©=0+1°¡ ![]() +2°¡
+2°¡ ![]() =
= ![]()
°æΩ‚Œˆ°ø£®1£©÷±Ω”¿˚”√k2‘ÀÀ„∑®‘Ú«ÛΩ‚£¨≈–∂œ…˙∂˛Ã•“‚‘∏”Ζ‘± «∑Ò”–πÿµƒΩ·¬€£ª£®2£©«Û≥ˆXµƒø…ƒÐ÷µ£¨«Û≥ˆ∏≈¬ £¨µ√µΩ∑÷≤º¡–£¨»ª∫Û«ÛΩ‚∆⁄Õ˚£Æ
°æøºµ„æ´Œˆ°øΩ‚¥¥Àµƒπÿº¸‘⁄”⁄¿ÌΩ‚¿Î…¢–ÕÀʪ˙±‰¡øº∞∆‰∑÷≤º¡–µƒœýπÿ÷™ ∂£¨’∆Œ’‘⁄…‰ª˜°¢≤˙∆∑ºÏ—ȵ»¿˝◊”÷–£¨∂‘”⁄Àʪ˙±‰¡øXø…ƒÐ»°µƒ÷µ£¨Œ“√«ø…“‘∞¥“ª∂®¥Œ–Ú“ª“ª¡–≥ˆ£¨’‚—˘µƒÀʪ˙±‰¡øΩ–◊ˆ¿Î…¢–ÕÀʪ˙±‰¡ø£Æ¿Î…¢–ÕÀʪ˙±‰¡øµƒ∑÷≤º¡–£∫“ª∞„µƒ,…Ë¿Î…¢–ÕÀʪ˙±‰¡øXø…ƒÐ»°µƒ÷µŒ™x1,x2,.....,xi,......,xn£¨X»°√ø“ª∏ˆ÷µ xi(i=1,2,......£©µƒ∏≈¬ P(¶Œ=xi£©£ΩPi£¨‘Ú≥∆±ÌŒ™¿Î…¢–ÕÀʪ˙±‰¡øX µƒ∏≈¬ ∑÷≤º£¨ºÚ≥∆∑÷≤º¡–£Æ


 ø™–ƒ ‘æÌ∆⁄ƒ©≥Â¥Ã100∑÷œµ¡–¥∞∏
ø™–ƒ ‘æÌ∆⁄ƒ©≥Â¥Ã100∑÷œµ¡–¥∞∏ À´ª˘Õ¨≤Ωµº∫Ω—µ¡∑œµ¡–¥∞∏
À´ª˘Õ¨≤Ωµº∫Ω—µ¡∑œµ¡–¥∞∏ ª∆∏‘–°◊¥‘™Õ¨≤Ωº∆À„ÃÏÃÏ¡∑œµ¡–¥∞∏
ª∆∏‘–°◊¥‘™Õ¨≤Ωº∆À„ÃÏÃÏ¡∑œµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øπ˝µ„£®0£¨2£©µƒ÷±œþl”Î÷––ƒ‘⁄‘≠µ„£¨Ω𵄑⁄x÷·…œ«“¿Î–ƒ¬ Œ™ ![]() µƒÕ÷‘≤CœýΩª”⁄A°¢B¡Ωµ„£¨÷±œþ
µƒÕ÷‘≤CœýΩª”⁄A°¢B¡Ωµ„£¨÷±œþ ![]() π˝œþ∂ŒABµƒ÷–µ„£¨Õ¨ ±Õ÷‘≤C…œ¥Ê‘⁄“ªµ„”Δ“Ωπµ„πÿ”⁄÷±œþl∂‘≥∆£Æ
π˝œþ∂ŒABµƒ÷–µ„£¨Õ¨ ±Õ÷‘≤C…œ¥Ê‘⁄“ªµ„”Δ“Ωπµ„πÿ”⁄÷±œþl∂‘≥∆£Æ
£®1£©«Û÷±œþlµƒ∑Ω≥ãª
£®2£©«ÛÕ÷‘≤Cµƒ∑Ω≥ãÆ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕºÀ˘ 棨»˝¿‚÷˘A1B1C1©ÅABCµƒ≤ý¿‚AA1°Õµ◊√ÊABC£¨AB°ÕAC£¨AB=AA1 £¨ D «¿‚CC1µƒ÷–µ„£Æ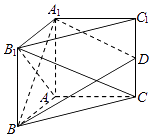
£®¢Ò£©÷§√˜£∫∆Ω√ÊAB1C°Õ∆Ω√ÊA1BD£ª
£®¢Ú£©‘⁄¿‚A1B1…œ «∑ҥʑ⁄“ªµ„E£¨ πC1E°Œ∆Ω√ÊA1BD£ø≤¢÷§√˜ƒ„µƒΩ·¬€£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨’˝Àƒ¿‚◊∂![]() ÷–£¨
÷–£¨ ![]() «’˝∑Ω–Œ£¨
«’˝∑Ω–Œ£¨ ![]() «’˝∑Ω–Œµƒ÷––ƒ£¨
«’˝∑Ω–Œµƒ÷––ƒ£¨ ![]() µ◊√Ê
µ◊√Ê![]() £¨
£¨ ![]() «
«![]() µƒ÷–µ„£Æ
µƒ÷–µ„£Æ
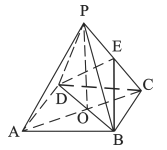
(I)÷§√˜£∫ ![]() ∆Ω√Ê
∆Ω√Ê![]() £ª
£ª
(II)÷§√˜£∫∆Ω√Ê![]() ∆Ω√Ê
∆Ω√Ê![]() £ª
£ª
(III)“—÷™£∫ ![]() £¨«Ûµ„
£¨«Ûµ„![]() µΩ√Ê
µΩ√Ê![]() µƒæý¿Î£Æ
µƒæý¿Î£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥–£Œ™¡ÀΩ‚1000√˚∏þ“ª–¬…˙µƒ…ÌÃÂ…˙≥§◊¥øˆ£¨”√œµÕ≥≥È—˘∑®£®∞¥µ»æýµƒπÊ‘Ú£©≥È»°40√˚Õ¨—ßΩ¯––ºÏ≤È£¨Ω´—ß…˙¥”1°´1000Ω¯––±ý∫≈£¨œ÷“—÷™µ⁄18◊È≥È»°µƒ∫≈¬ÎŒ™443£¨‘Úµ⁄“ª◊È”√ºÚµ•Àʪ˙≥È—˘≥È»°µƒ∫≈¬ÎŒ™ £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄±þ≥§Œ™1µƒ’˝∑Ω–Œƒ⁄◊˜¡Ω∏ˆª•œýÕ‚«–µƒ‘≤£¨Õ¨ ±√ø“ª∏ˆ‘≤”÷”Î’˝∑Ω–Œµƒ¡Ωœý¡⁄±þœý«–£¨µ±“ª∏ˆ‘≤Œ™’˝∑Ω–Œƒ⁄«–‘≤ ±∞Îæ∂◊Ó¥Û£¨¡Ì“ª‘≤∞Îæ∂◊Ó–°£¨º«∆‰÷–“ª∏ˆ‘≤µƒ∞Îæ∂Œ™x£¨¡Ω‘≤µƒ√ʪ˝÷Æ∫ÕŒ™S£¨Ω´S±Ì 挙xµƒ∫Ø ˝°£
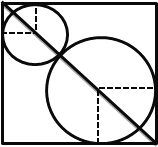
«Û£∫£®1£©∫Ø ˝![]() µƒΩ‚Œˆ Ω£ª
µƒΩ‚Œˆ Ω£ª
£®2£©![]() µƒ÷µ”Ú.
µƒ÷µ”Ú.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄»˝¿‚÷˘![]() ÷–£¨
÷–£¨ ![]() ∆Ω√Ê
∆Ω√Ê![]() £¨
£¨ ![]() £¨
£¨ ![]() ‘⁄œþ∂Œ
‘⁄œþ∂Œ![]() …œ£¨
…œ£¨ ![]() £¨
£¨ ![]() .
.
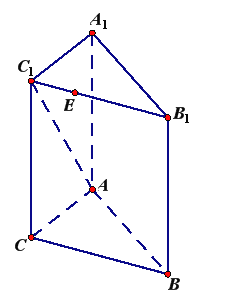
£®1£©«Û÷§£∫ ![]() £ª
£ª
£®2£© ‘ÃΩæø£∫‘⁄![]() …œ «∑ҥʑ⁄µ„
…œ «∑ҥʑ⁄µ„![]() £¨¬˙◊„
£¨¬˙◊„![]() ∆Ω√Ê
∆Ω√Ê![]() £¨»Ù¥Ê‘⁄£¨«Î÷∏≥ˆµ„
£¨»Ù¥Ê‘⁄£¨«Î÷∏≥ˆµ„![]() µƒŒª÷√£¨≤¢∏¯≥ˆ÷§√˜£ª»Ù≤ª¥Ê‘⁄£¨Àµ√˜¿Ì”….
µƒŒª÷√£¨≤¢∏¯≥ˆ÷§√˜£ª»Ù≤ª¥Ê‘⁄£¨Àµ√˜¿Ì”….
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø¥ÛŒ˜—ÛˆŸ”„√øƒÍ∂º“™ƒÊ¡˜∂¯…œ£¨”Œªÿ≤˙µÿ≤˙¬—£¨—–æøˆŸ”„µƒø∆—ߺ“∑¢œ÷ˆŸ”„µƒ”ŒÀŸ![]() £®µ•Œª£∫
£®µ•Œª£∫ ![]() £©”Î∆‰∫ƒ—ı¡øµ•Œª ˝
£©”Î∆‰∫ƒ—ı¡øµ•Œª ˝![]() ÷ƺ‰µƒπÿœµø…“‘±Ì 挙∫Ø ˝
÷ƺ‰µƒπÿœµø…“‘±Ì 挙∫Ø ˝![]() £¨∆‰÷–
£¨∆‰÷–![]() Œ™≥£ ˝£¨“—÷™“ªÃıˆŸ”„‘⁄æ≤÷π ±µƒ∫ƒ—ı¡øŒ™100∏ˆµ•Œª£ª∂¯µ±À¸µƒ”ŒÀŸŒ™
Œ™≥£ ˝£¨“—÷™“ªÃıˆŸ”„‘⁄æ≤÷π ±µƒ∫ƒ—ı¡øŒ™100∏ˆµ•Œª£ª∂¯µ±À¸µƒ”ŒÀŸŒ™![]() ±£¨∆‰∫ƒ—ı¡øŒ™2700∏ˆµ•Œª.
±£¨∆‰∫ƒ—ı¡øŒ™2700∏ˆµ•Œª.
£®1£©«Û≥ˆ”ŒÀŸ![]() ”Î∆‰∫ƒ—ı¡øµ•Œª ˝
”Î∆‰∫ƒ—ı¡øµ•Œª ˝![]() ÷ƺ‰µƒ∫Ø ˝Ω‚Œˆ Ω£ª
÷ƺ‰µƒ∫Ø ˝Ω‚Œˆ Ω£ª
£®2£©«Ûµ±“ªÃıˆŸ”„µƒ”ŒÀŸ≤ª∏þ”⁄![]() ±£¨∆‰∫ƒ—ı¡ø÷¡∂ý–Ë“™∂ý…Ÿ∏ˆµ•Œª£ø
±£¨∆‰∫ƒ—ı¡ø÷¡∂ý–Ë“™∂ý…Ÿ∏ˆµ•Œª£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕºÀ˘ 棨‘⁄¿‚≥§Œ™4µƒ’˝∑ΩÃÂABCD©ÅA1B1C1D1÷–£¨µ„E «¿‚CC1µƒ÷–µ„£¨‘Ú“Ï√Ê÷±œþD1E”ÎACÀ˘≥…Ω«µƒ”ýœ“÷µ « £Æ 
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com