Question

6．已知△OAB的直观图△O′A′B′（如图）O′A′=1，∠B′=30°，则△OAB的面积为（　　）

• A． $\sqrt{6}$
• B． $\frac{\sqrt{3}}{2}$
• C． $\frac{\sqrt{6}}{2}$
• D． $\sqrt{3}$

Answer 1

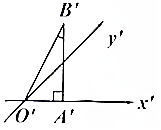
分析 由已知中Rt△O′A′B′是一平面图形的直观图，O′A′=1，∠B′=30°，我们易求出Rt△O′A′B′的面积，再根据原图的面积与直观图面积之比为1：$\frac{\sqrt{2}}{4}$，即可求出满足条件答案．

解答 解：由已知中Rt△O′A′B′，O′A′=1，∠B′=30°，则Rt△O′A′B′的面积S=$\frac{1}{2}×1×\sqrt{3}$=$\frac{\sqrt{3}}{2}$，
由原图的面积与直观图面积之比为1：$\frac{\sqrt{2}}{4}$，
可得原图形的面积为：$\sqrt{6}$
故选：A．

点评 本题考查的知识点是平面图形的直观图，其中原图的面积与直观图面积之比为1：$\frac{\sqrt{2}}{4}$，是解答此类问题的关键．