
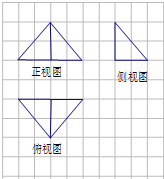
| A. | $\frac{8}{3}π$ | B. | 8π | C. | $\frac{32}{3}π$ | D. | $\frac{16}{3}π$ |
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
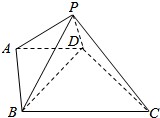 直角梯形ABCD中,∠ABC=90°,AB=AD=AP=1,BC=2,平面ABP垂直于底面ABCD.
直角梯形ABCD中,∠ABC=90°,AB=AD=AP=1,BC=2,平面ABP垂直于底面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在平行四边形么BCD中,∠DAB=60°,AD=4,AB=2,将△CBD沿BD折起到△EBD的位置.
如图,在平行四边形么BCD中,∠DAB=60°,AD=4,AB=2,将△CBD沿BD折起到△EBD的位置.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “所有金属都能导电,铁是金属,所以铁能导电”这种推理属于演绎推理 | |
| B. | 已知数据x1,x2,…,xn的方差是4,则数据-3x1+2015,-3x2+2015,…,-3xn+2015的标准差是6 | |
| C. | 用相关指数R2来刻画回归效果,R2的值越小,说明模型的拟合效果越好 | |
| D. | 若变量y和x之间的相关系数r=-0.9362,则变量y和x之间具有很强的线性相关关系 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
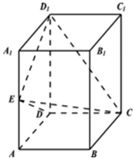 (Ⅰ)证明:A1B1∥平面CDE;
(Ⅰ)证明:A1B1∥平面CDE;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com