
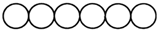 用红黄蓝三种颜色给如图所示的六连圆涂色,若每种颜色只能涂两个圆,且相邻两个圆所涂颜色不能相同,则不同的涂色方案共有
用红黄蓝三种颜色给如图所示的六连圆涂色,若每种颜色只能涂两个圆,且相邻两个圆所涂颜色不能相同,则不同的涂色方案共有科目:高中数学 来源: 题型:
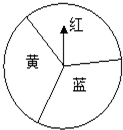 如图一个圆盘被三等分,分别涂上红黄蓝三种颜色,小明和小亮用的这一个转盘进行“配紫色”游戏.游戏规则如下:每次任意转动转盘,再等转盘停止时,指针指向哪种颜色,结果就记为这种颜色,连续转动两次转盘,如果两次转盘转出的颜色相同或配成紫色(若其中一次转盘转出蓝色,另一次转出红色,则可配成紫色),则小明得1分,否则小亮得1分.试问:
如图一个圆盘被三等分,分别涂上红黄蓝三种颜色,小明和小亮用的这一个转盘进行“配紫色”游戏.游戏规则如下:每次任意转动转盘,再等转盘停止时,指针指向哪种颜色,结果就记为这种颜色,连续转动两次转盘,如果两次转盘转出的颜色相同或配成紫色(若其中一次转盘转出蓝色,另一次转出红色,则可配成紫色),则小明得1分,否则小亮得1分.试问:查看答案和解析>>
科目:高中数学 来源:2012年浙江省温州市高考数学二模试卷(理科)(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com