
【题目】未来制造业对零件的精度要求越来越高. ![]() 打印通常是采用数字技术材料打印机来实现的,常在模具 制造、工业设计等领域被用于制造模型,后逐渐用于一些产品的直接制造,已经有使用这种技术打印而成的零部件.该技术应用十分广泛,可以预计在未来会有广阔的发展空间.某制造企业向
打印通常是采用数字技术材料打印机来实现的,常在模具 制造、工业设计等领域被用于制造模型,后逐渐用于一些产品的直接制造,已经有使用这种技术打印而成的零部件.该技术应用十分广泛,可以预计在未来会有广阔的发展空间.某制造企业向![]() 高校
高校![]() 打印实验团队租用一台
打印实验团队租用一台![]() 打印设备,用于打印一批对内径有较高精度要求的零件.该团队在实验室打印出了一批这样的零件,从中随机抽取10件零件,度量其内径的茎叶图如图所示(单位:
打印设备,用于打印一批对内径有较高精度要求的零件.该团队在实验室打印出了一批这样的零件,从中随机抽取10件零件,度量其内径的茎叶图如图所示(单位: ![]() ).
).
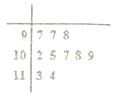
(1)计算平均值![]() 与标准差
与标准差![]() ;
;
(2)假设这台![]() 打印设备打印出品的零件内径
打印设备打印出品的零件内径![]() 服从正态分布
服从正态分布![]() ,在抽检零件中,如果出现了尺寸在
,在抽检零件中,如果出现了尺寸在![]() 之外的零件,就认为打印过程可能出现了异常情况,需对打印设备进行检查再调试.该团队到工厂安装调试后,试打了5个零件.度量其内径分别为(单位:
之外的零件,就认为打印过程可能出现了异常情况,需对打印设备进行检查再调试.该团队到工厂安装调试后,试打了5个零件.度量其内径分别为(单位: ![]() ): 86、95、103、109、118,试问此打印设备是否需要进一步调试,为什么?
): 86、95、103、109、118,试问此打印设备是否需要进一步调试,为什么?
参考数据: ![]() ,
, ![]() ,
,
![]() .
.
科目:高中数学 来源: 题型:
【题目】下列各式中,正确的是( )
A.2{x|x≤2}
B.3∈{x|x>2且x<1}
C.{x|x=4k±1,k∈Z}≠{x|x=2k+1,k∈Z}
D.{x|x=3k+1,k∈Z}={x|x=3k﹣2,k∈Z}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱.为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计60吨厨余垃圾,假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱和“其他垃圾”箱的投放量分别为x,y,z,其中x>0,x+y+z=60,则数据x,y,z的标准差的最大值为 . (注:方差 ![]() ,其中
,其中 ![]() 为x1 , x2 , …,xn的平均数)
为x1 , x2 , …,xn的平均数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的偶函数,f(x)在[0,+∞)上是增函数,且f( ![]() )=0,则不等式f(
)=0,则不等式f( ![]() )>0的解集为( )
)>0的解集为( )
A.(0, ![]() )∪(2,+∞)
)∪(2,+∞)
B.( ![]() ,1)∪(2,+∞)??
,1)∪(2,+∞)??
C.(0, ![]() )
)
D.(2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点M(x,y)与定点F(1,0)的距离和它到直线l:x=2的距离的比为 ![]() ,
,
(Ⅰ)求点M的轨迹.
(Ⅱ)是否存在点M到直线 ![]() +y=1的距离最大?最大距离是多少?
+y=1的距离最大?最大距离是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆方程![]() 为:
为: ![]() ,
, ![]() 椭圆的右焦点为
椭圆的右焦点为![]() ,离心率为
,离心率为![]() ,直线
,直线![]() :
: ![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]()
(1)椭圆的方程及求![]() 的面积;
的面积;
(2)在椭圆上是否存在一点![]() ,使
,使![]() 为平行四边形,若存在,求出
为平行四边形,若存在,求出![]() 的取值范围,若不存在说明理由.
的取值范围,若不存在说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com