
(本题满分14分)某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入1 00元,已知总收益满足函数:
00元,已知总收益满足函数: ,其中
,其中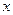 是仪器的月产量。
是仪器的月产量。
(1)将利润表示为月产量的函数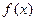 ;
;
(2)当月产量为何值时,公司所获利润最大?最大利润为多少元?
(利润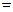 总收益
总收益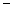 总成本)
总成本)
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:解答题
(本小题共12分)
已知函数f(x)=2x-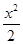 -aln(x+1),a∈R.(1)若a=-4,求函数f(x)的单调区间;
-aln(x+1),a∈R.(1)若a=-4,求函数f(x)的单调区间;
(2)求y=f(x)的极值点(即函数取到极值时点的横坐标).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某厂家拟在2010年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量) 万件与促销费用
万件与促销费用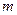 万元(
万元(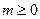 )满足
)满足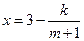 (
(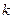 为常数),如果不搞促销活动,则该产品的年销量只能是1万件。已知2010年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品的年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金)。
为常数),如果不搞促销活动,则该产品的年销量只能是1万件。已知2010年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品的年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金)。
(1)将2010年该产品的利润y万元表示为年促销费用m万元的函数;
(2)该厂家2010年的促销费用投入多少万元时,厂家的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)某新型智能在线电池的电量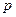 (单位:kwh)随时间
(单位:kwh)随时间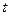 (单位:小时)的变化规律是:
(单位:小时)的变化规律是: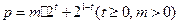 ,其中
,其中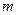 是智能芯片实时控制的参数。
是智能芯片实时控制的参数。
(1)当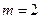 时,求经过多少时间电池电量是
时,求经过多少时间电池电量是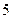 kwh;
kwh;
(2)如果电池的电量始终不低于2 kwh,求参数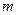 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分14分)
已知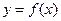 是定义在R上的偶函数,当
是定义在R上的偶函数,当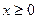 时,
时,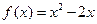
(1)求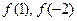 的值;
的值;
⑵求 的解析式并画出简图;
的解析式并画出简图;
⑶讨论方程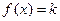 的根的情况。(只需写出结果,不要解答过程).
的根的情况。(只需写出结果,不要解答过程).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(理数)(12分)某商场销售 某种商品的经验表明,该商品每日的销售量
某种商品的经验表明,该商品每日的销售量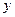 (单位:千克)与销售价格
(单位:千克)与销售价格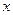 (单位:元/千克)满
(单位:元/千克)满 足关系式
足关系式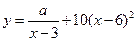 ,其中
,其中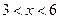 ,
,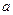 为常数,已知销售价格为5元/千克时,每日可售出该商品11千克
为常数,已知销售价格为5元/千克时,每日可售出该商品11千克
(Ⅰ) 求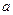 的值;
的值;
(Ⅱ) 若该商品的成品为3元/千克, 试确定销售价格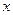 的值,使商场每日销售该
的值,使商场每日销售该 商品所获得的利润最大.
商品所获得的利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知一家公司生产某种品牌服装的年固定成本为10万元,每生产1千件需另投入2.7万元.设该公司一年内共生产该品牌服装x千件并全部销售完,每千件的销售收入为R(x)万元,且R(x)=
(1)写出年利润W(万元)关于年产量x(千件)的函数解析式;
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获得利润最大?(注:年利润=年销售收入-年总成本)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com