
【题目】在直角△ABC中,∠ACB=30°,∠B=90°,D为AC中点(左图),将∠ABD沿BD折起,使得AB⊥CD(右图),则二面角A﹣BD﹣C的余弦值为( ) 
A.﹣ ![]()
B.![]()
C.﹣ ![]()
D.![]()
【答案】A
【解析】解:过A作AE⊥BD,在原图延长角BC与F,过A作AO⊥面BCD,垂足为O.由于面AEF⊥面BCD,所以O在FE上,连BO交CD延长线于M,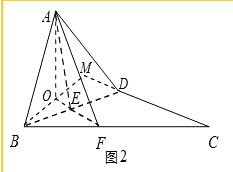
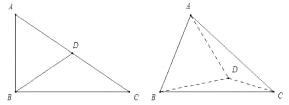
∵在△ABC中,∠ACB=30°,∠B=90°,D为AC中点,
AB= ![]() ,BD=
,BD= ![]() AC,
AC,
∴△ABD为等边三角形,
∴BD⊥AE,BD⊥EF,
∴∠AEF为二面角A﹣BD﹣C的平面角,
过A作AO⊥面BCD,垂足为O,
∵面AEF⊥面BCD,
∴O在EF上,
理解BO交CD延长线于M,
当AB⊥CD时,由三垂线定理的逆定理可知:MB⊥CM,
∴O为翻折之前的三角形ABD的中心,
∴OE= ![]() AE,
AE,
cos∠AEO= ![]() ,
,
∴cos∠AEF= ![]() ,
,
故选:A


科目:高中数学 来源: 题型:
【题目】已知数列{an}的首项为1,前n项和Sn与an之间满足an= ![]() (n≥2,n∈N*)
(n≥2,n∈N*)
(1)求证:数列{ ![]() }是等差数列;
}是等差数列;
(2)求数列{an}的通项公式;
(3)设存在正整数k,使(1+S1)(1+S1)…(1+Sn)≥k ![]() 对于一切n∈N*都成立,求k的最大值.
对于一切n∈N*都成立,求k的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0),其部分图象如图所示,点P,Q分别为图象上相邻的最高点与最低点,R是图象与x轴的交点,若P点的横坐标为 ![]() ,f(
,f( ![]() )=
)= ![]() ,PR⊥QR,则函数f(x)的解析式可以是( )
,PR⊥QR,则函数f(x)的解析式可以是( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线系M:xcosθ+(y﹣1)sinθ=1(0≤θ≤2π),对于下列说法:
(1)M中所有直线均经过一个定点;
(2)存在一个圆与所有直线不相交;
(3)对于任意整数n(n≥3),存在正n边形,其所有边均在M中的直线上;
(4)M中的直线所能围成的正三角形面积都相等.
其中说法正确的是(填序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且Sn+an=4,n∈N* .
(1)求数列{an}的通项公式;
(2)已知cn=2n+3(n∈N*),记dn=cn+logCan(C>0且C≠1),是否存在这样的常数C,使得数列{dn}是常数列,若存在,求出C的值;若不存在,请说明理由.
(3)若数列{bn},对于任意的正整数n,均有b1an+b2an﹣1+b3an﹣2+…+bna1=( ![]() )n﹣
)n﹣ ![]() 成立,求证:数列{bn}是等差数列.
成立,求证:数列{bn}是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1 , F2分别为双曲线C: ![]() ﹣
﹣ ![]() =1的左、右焦点,若存在过F1的直线分别交双曲线C的左、右支于A,B两点,使得∠BAF2=∠BF2F1 , 则双曲线C的离心率e的取值范围是( )
=1的左、右焦点,若存在过F1的直线分别交双曲线C的左、右支于A,B两点,使得∠BAF2=∠BF2F1 , 则双曲线C的离心率e的取值范围是( ) 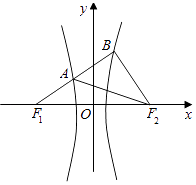
A.(3,+∞)
B.(1,2+ ![]() )
)
C.(3,2+ ![]() )
)
D.(1,3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com