Question

13．已知圆O为Rt△ABC的内切圆，AC=3，BC=4，∠C=90°，过圆心O的直线l交圆O于P，Q两点，则$\overrightarrow{BP}•\overrightarrow{CQ}$的取值范围是（　　）

• A． （-7，1）
• B． ．[0，1]
• C． [-7，0]
• D． [-7，1]

Answer 1

分析 以O为坐标原点，与直线BC平行的直线为x轴，与直线AC平行的直线为y轴，建立直角坐标系，设△ABC的内切圆的半径为r，运用面积相等可得r=1，设出圆的方程，求得交点P，Q，讨论直线的斜率k不存在和大于0，小于0的情况，运用向量的坐标运算，结合数量积的坐标表示和不等式的性质，计算即可得到范围．

解答 解：以O为坐标原点，与直线BC平行的直线为x轴，
与直线AC平行的直线为y轴，建立直角坐标系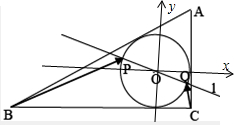，如图所示；
设△ABC的内切圆的半径为r，
运用面积相等可得，$\frac{1}{2}$×3×4=$\frac{1}{2}$×r×（3+4+5），
解得r=1，
则B（-3，-1），C（1，-1），
即有圆O：x²+y²=1，
当直线PQ的斜率不存在时，即有P（0，1），Q（0，-1），
$\overrightarrow{BP}$=（3，3），$\overrightarrow{CQ}$=（-1，0），即有$\overrightarrow{BP}$=-3．
当直线PQ的斜率存在时，设直线l：y=kx，（k＜0），
代入圆的方程可得P（-$\frac{1}{\sqrt{1{+k}^{2}}}$，-$\frac{k}{\sqrt{1{+k}^{2}}}$），Q（$\frac{1}{\sqrt{1{+k}^{2}}}$，$\frac{k}{\sqrt{1{+k}^{2}}}$），
即有$\overrightarrow{BP}$=（3-$\frac{1}{\sqrt{1{+k}^{2}}}$，1-$\frac{k}{\sqrt{1{+k}^{2}}}$），$\overrightarrow{CQ}$=（$\frac{1}{\sqrt{1{+k}^{2}}}$-1，$\frac{k}{\sqrt{1{+k}^{2}}}$+1），
则有$\overrightarrow{BP}$=（3-$\frac{1}{\sqrt{1{+k}^{2}}}$）（$\frac{1}{\sqrt{1{+k}^{2}}}$-1）+（1-$\frac{k}{\sqrt{1{+k}^{2}}}$）（$\frac{k}{\sqrt{1{+k}^{2}}}$+1）
=-3+$\frac{4}{\sqrt{1{+k}^{2}}}$，
由1+k²≥1可得0＜$\frac{4}{\sqrt{1{+k}^{2}}}$≤4，
则有-3＜-3+$\frac{4}{\sqrt{1{+k}^{2}}}$≤1；
同理当k＞0时，求得P（$\frac{1}{\sqrt{1{+k}^{2}}}$，$\frac{k}{\sqrt{1{+k}^{2}}}$），Q（-$\frac{1}{\sqrt{1{+k}^{2}}}$，-$\frac{k}{\sqrt{1{+k}^{2}}}$），
有$\overrightarrow{BP}$═-3-$\frac{4}{\sqrt{1{+k}^{2}}}$，
可得-7≤-3+$\frac{4}{\sqrt{1{+k}^{2}}}$＜-3；
综上可得，$\overrightarrow{BP}$•$\overrightarrow{CQ}$的取值范围是[-7，1]．
故选：D．

点评 本题考查了向量的数量积坐标表示，主要考查向量的坐标运算和直线与圆的位置关系以及不等式的性质问题，是综合性题目．