
【题目】选修4—4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).以原点为极点,
为参数).以原点为极点,![]() 轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆![]() 的方程为
的方程为![]() .
.
(Ⅰ)写出直线![]() 的普通方程和圆
的普通方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若点![]() 的直角坐标为
的直角坐标为![]() ,圆
,圆![]() 与直线
与直线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】衡州市临枣中学高二某小组随机调查芙蓉社区160个人,以研究这一社区居民在20:00-22:00时间段的休闲方式与性别的关系,得到下面的数据表:
休闲方式 性别 | 看电视 | 看书 | 合计 |
男 | 20 | 100 | 120 |
女 | 20 | 20 | 40 |
合计 | 40 | 120 | 160 |
下面临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
(Ⅰ)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,设调查的3人在这一时间段以看书为休闲方式的人数为随机变量![]() ,求
,求![]() 的分别列和期望;
的分别列和期望;
(Ⅱ)根据以上数据,能否有99%的把握认为“在20:00-22:00时间段的休闲方式与性别有关系”?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 是椭圆
是椭圆![]() 的右焦点,直线
的右焦点,直线![]() 的斜率为
的斜率为![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)求![]() 的方程;
的方程;
(2)设过点![]() 的动直线
的动直线![]() 与
与![]() 相交于
相交于![]() 两点,问:是否存在直线
两点,问:是否存在直线![]() ,使以
,使以![]() 为直径的圆经过原点
为直径的圆经过原点![]() ,若存在,求出对应直线
,若存在,求出对应直线![]() 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某初级中学有三个年级,各年级男、女人数如下表:
初一年级 | 初二年级 | 初三年级 | |
女生 | 370 |
| 200 |
男生 | 380 | 370 | 300 |
已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19.
(1)求![]() 的值;
的值;
(2)用分层抽样的方法在初三年级中抽取一个容量为5的样本,求该样本中女生的人数;
(3)用随机抽样的方法从初二年级女生中选出8人,测量它们的左眼视力,结果如下:1.2,1.5,1.2,1.5,1.5,1.3,1.0,1.2.把这8人的左眼视力看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.1的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究小组在电脑上进行人工降雨模拟实验,准备用![]() 、
、![]() 、
、![]() 三种人工降雨方式分别对甲、乙、丙三地实施人工降雨,其试验数据统计如表:
三种人工降雨方式分别对甲、乙、丙三地实施人工降雨,其试验数据统计如表:
方式 | 实施地点 | 大雨 | 中雨 | 小雨 | 模拟实验总次数 |
| 甲 | 4次 | 6次 | 2次 | 12次 |
| 乙 | 3次 | 6次 | 3次 | 12次 |
| 丙 | 2次 | 2次 | 8次 | 12次 |
假定对甲、乙、丙三地实施的人工降雨彼此互不影响,请你根据人工降雨模拟实验的统计数据:
(Ⅰ)求甲、乙、丙三地都恰为中雨的概率;
(Ⅱ)考虑到旱情和水土流失,如果甲地恰需中雨即达到理想状态,乙地必须是大雨才达到理想状态,丙地只能是小雨或中雨即达到理想状态,记“甲、乙、丙三地中达到理想状态的个数”为随机变量![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学举行了一次“环保知识竞赛”, 全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
![]()
| 分组 | 频数 | 频率 |
第1组 | [50,60) | 8 | 0 16 |
第2组 | [60,70) | a | ▓ |
第3组 | [70,80) | 20 | 0 40 |
第4组 | [80,90) | ▓ | 0 08 |
第5组 | [90,100] | 2 | b |
合计 | ▓ | ▓ |

(1)求出![]() 的值;
的值;
(2)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学到广场参加环保知识的志愿宣传活动
(ⅰ)求所抽取的2名同学中至少有1名同学来自第5组的概率;
(ⅱ)求所抽取的2名同学来自同一组的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在以![]() 为顶点的五面体中,O为AB的中点,
为顶点的五面体中,O为AB的中点,
![]() 平面
平面![]() ,
, ![]() ∥
∥![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(1)在图中过点O作平面![]() ,使得
,使得![]() ∥平面
∥平面![]() ,并说明理由;
,并说明理由;
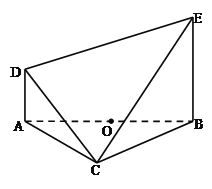
(2)求直线DE与平面CBE所成角的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com