
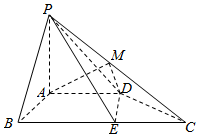
 ��ͼ��������P-ABCD�У�PA��ƽ��ABCD��PA=AB=AD=2���ı���ABCD����AB��AD��BC��AD��BC=4����MΪPC�е㣬��EΪBC���ϵĶ��㣬��$\frac{BE}{EC}=��$��
��ͼ��������P-ABCD�У�PA��ƽ��ABCD��PA=AB=AD=2���ı���ABCD����AB��AD��BC��AD��BC=4����MΪPC�е㣬��EΪBC���ϵĶ��㣬��$\frac{BE}{EC}=��$������ ������AΪԭ�㣬��AB��AD��AP����ֱ�߷ֱ�Ϊx�ᣬy�ᣬz�Ὠ���ռ�ֱ������ϵ��������������֤��DM��ƽ��PAB��
�������ƽ��ADM��һ����������ƽ��PBC��һ����������������������֤��ƽ��ADM��ƽ��PBC��
�������ƽ��PDE�ķ�������ƽ��DEB�ķ�����������������������˵�ֵ��
��� 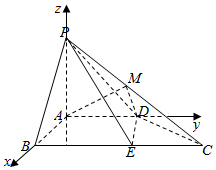 ֤����������AΪԭ�㣬��AB��AD��AP����ֱ�߷ֱ�Ϊx�ᣬy�ᣬz�Ὠ���ռ�ֱ������ϵ������1�֣�
֤����������AΪԭ�㣬��AB��AD��AP����ֱ�߷ֱ�Ϊx�ᣬy�ᣬz�Ὠ���ռ�ֱ������ϵ������1�֣�
������ã�D��0��2��0����C��2��4��0����P��0��0��2����M��1��2��1����A��0��0��0����B��2��0��0����
$\overrightarrow{DM}$=��1��0��1����ƽ��PAB�ķ�����$\overrightarrow{n}$=��0��1��0����
��$\overrightarrow{DM}•\overrightarrow{n}$=0��DM?ƽ��PAB��
��DM��ƽ��PAB���� ����4�֣�
�⣺������ƽ��ADM��һ��������$\overrightarrow{m}$=��x��y��z����
$\overrightarrow{AD}$=��0��2��0����$\overrightarrow{AM}$=��1��2��1����
��$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AD}=2y=0}\\{\overrightarrow{m}•\overrightarrow{AM}=x+2y+z=0}\end{array}\right.$��ȡx=1����$\overrightarrow{m}$=��1��0��-1����
��ƽ��PBC��һ��������$\overrightarrow{p}$=��x��y��z����
$\overrightarrow{PB}$=��2��0��0����$\overrightarrow{PC}$=��2��4��0����
��$\left\{\begin{array}{l}{\overrightarrow{p}•\overrightarrow{PB}=2x-2z=0}\\{\overrightarrow{p}•\overrightarrow{PC}=2x+4y-2z=0}\end{array}\right.$��ȡx=1����$\overrightarrow{p}$=��1��0��1����
��$\overrightarrow{m}•\overrightarrow{p}$=0��
��ƽ��ADM��ƽ��PBC������8�֣�
�����ڷ��������Ħˣ�
��E��2��t��0����P��0��0��2����D��0��2��0����B��2��0��0��
��$\overrightarrow{PD}$=��0��-2��2����$\overrightarrow{DE}$=��2��t-2��0����
��ƽ��PDE�ķ�����Ϊ$\overrightarrow{q}$=��a��b��c����
$\left\{\begin{array}{l}{\overrightarrow{q}•\overrightarrow{PD}=-2b+2c=0}\\{\overrightarrow{q}•\overrightarrow{DE}=2a+��t-2��b=0}\end{array}\right.$��ȡb=2����$\overrightarrow{q}$=��2-t��2��2����
��ƽ��DEB��ΪxAyƽ�棬�䷨����$\overrightarrow{v}$=��0��0��1����
��߶����P-DE-B������ֵΪ$\frac{2}{3}$��
��|cos��$\overrightarrow{q}��\overrightarrow{v}$��|=|$\frac{\overrightarrow{q}•\overrightarrow{v}}{|\overrightarrow{q}|•|\overrightarrow{v}|}$|=$\frac{2}{\sqrt{��2-t��^{2}+8}}$=$\frac{2}{3}$��
���t=3��t=1��������=3���=$\frac{1}{3}$������13�֣�
���� ��С����Ҫ�������弸�ε����֪ʶ�������漰�������Լ�����Ĵ�ֱ��ϵ������ǵ����ռ����������弸���е�Ӧ�ã���С��Կ����Ŀռ�����������������������нϸ�Ҫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2016-2017ѧ�����ɹŸ߶������¿�һ��ѧ���Ծ��������棩 ���ͣ�ѡ����
��֪˫����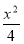 -
-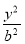 =1���ҽ�����������y2=12x�Ľ����غϣ����˫���ߵĽ��㵽�佥���ߵľ�����ڣ� ��
=1���ҽ�����������y2=12x�Ľ����غϣ����˫���ߵĽ��㵽�佥���ߵľ�����ڣ� ��
A. B.4
B.4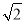 C.3 D.5
C.3 D.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ�꽭������һ�и߶��϶ο�һ��ѧ�������Ծ��������棩 ���ͣ�ѡ����
��֪Բ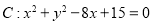 ��ֱ��
��ֱ��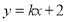 �����ٴ���һ��
�����ٴ���һ��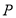 ��ʹ���Ե�
��ʹ���Ե�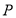 Ϊԭ�ģ��뾶Ϊ1��Բ��Բ
Ϊԭ�ģ��뾶Ϊ1��Բ��Բ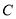 �й����㣬��
�й����㣬��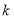 ����Сֵ�ǣ� ��
����Сֵ�ǣ� ��
A.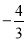 B.
B.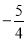 C.
C.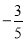 D.
D.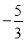
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
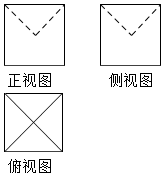 ij�����������ͼ��ͼ��ʾ��ͼ�е��ı��ζ��DZ߳�Ϊ2�������Σ����������ഹֱ����ȣ���ü����������ǣ�������
ij�����������ͼ��ͼ��ʾ��ͼ�е��ı��ζ��DZ߳�Ϊ2�������Σ����������ഹֱ����ȣ���ü����������ǣ�������| A�� | $\frac{20}{3}$ | B�� | $\frac{16}{3}$ | C�� | $8-\frac{��}{6}$ | D�� | $8-\frac{��}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��б������ABC-A1B1C1�ĵ�����ֱ�������Σ���ACB=90�㣬��B1�ڵ���ABC�ϵ���ӰǡΪBC���е㣬��BC=CA=AA1��
��ͼ��б������ABC-A1B1C1�ĵ�����ֱ�������Σ���ACB=90�㣬��B1�ڵ���ABC�ϵ���ӰǡΪBC���е㣬��BC=CA=AA1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
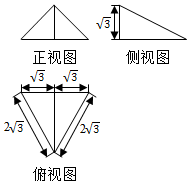
| A�� | 20�� | B�� | 19�� | C�� | 16�� | D�� | 12�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
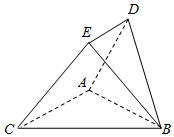 ��ͼ����BCΪб�ߵĵ���ֱ��������ABC��ȱ�������ABD����ƽ�滥�ഹֱ���ҵ�E����$\overrightarrow{DE}$=$\frac{1}{2}$$\overrightarrow{AC}$��
��ͼ����BCΪб�ߵĵ���ֱ��������ABC��ȱ�������ABD����ƽ�滥�ഹֱ���ҵ�E����$\overrightarrow{DE}$=$\frac{1}{2}$$\overrightarrow{AC}$���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com