
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| e |
| 6 |
| a |
| 2 |
| e |
| 2 |
| a |
| 2 |
| e |
| 2 |
| e |
| 2 |
| e |
| 2 |
| a |
| 2 |
| e |
|
| 2 |
| x |
| ax-2 |
| x |
| 2 |
| a |
| 2 |
| e |
| 6 |
| e |
| 2 |
| e |
| 2 |
| a |
| 2 |
| e |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
A、
| ||||
B、
| ||||
| C、36 | ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| OM |
| AB |
| A、(-1,3,-3) |
| B、(1,-3,3) |
| C、(9,1,1) |
| D、(-9,-1,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:
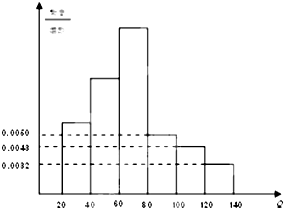 中华人民共和国《道路交通安全法》中将饮酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其检测标准是驾驶人员血液中的酒精含量Q(简称血酒含量,单位是毫克/100毫升),当20≤Q≤80时,为酒后驾车;当Q>80时,为醉酒驾车.某 市公安局交通管理部门于2014年1月的某天晚上8点至11点设点进行一次拦查行动,共依法查出了40名饮酒后违法驾驶机动车者,如图为这40名驾驶员抽血检测后所得结果画出的频率分布直方图(其中Q≥140的人数计入120≤Q<140人数之内.小矩形从低到高的高度依次为0.0032 0.0043 0.0050 0.0090 0.0125 0.016).
中华人民共和国《道路交通安全法》中将饮酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其检测标准是驾驶人员血液中的酒精含量Q(简称血酒含量,单位是毫克/100毫升),当20≤Q≤80时,为酒后驾车;当Q>80时,为醉酒驾车.某 市公安局交通管理部门于2014年1月的某天晚上8点至11点设点进行一次拦查行动,共依法查出了40名饮酒后违法驾驶机动车者,如图为这40名驾驶员抽血检测后所得结果画出的频率分布直方图(其中Q≥140的人数计入120≤Q<140人数之内.小矩形从低到高的高度依次为0.0032 0.0043 0.0050 0.0090 0.0125 0.016).查看答案和解析>>
科目:高中数学 来源: 题型:
| A、(x+2)2+2y2=4 |
| B、(x+2)2+2y2=4(-1<x≤0) |
| C、x2+2(y+2)2=4 |
| D、x2+2(y+2)2=4(-1<x≤0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com