练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．已知tanx=2，则$\frac{sin2x+2cos2x}{{2{{cos}^2}x-3sin2x-1}}$的值为$\frac{2}{15}$．

    分析 利用二倍角公式及同角的三角函数关系式的应用即可化简求值．

    解答 解：∵tanx=2，
    ∴$\frac{sin2x+2cos2x}{{2{{cos}^2}x-3sin2x-1}}$=$\frac{sin2x+2cos2x}{cos2x-3sin2x}$=$\frac{2sinxcosx+2co{s}^{2}x-2si{n}^{2}x}{co{s}^{2}x-si{n}^{2}x-6sinxcosx}$=$\frac{2tanx+2-2ta{n}^{2}x}{1-ta{n}^{2}x-6tanx}$=$\frac{4+2-8}{1-4-12}$=$\frac{2}{15}$．
    故答案为：$\frac{2}{15}$．

    点评 本题主要考查了二倍角公式及同角的三角函数关系式的应用，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    2．已知函数f（x）=1-$\frac{2}{1{0}^{x}+1}$．
    （1）判断函数f（x）的奇偶性；
    （2）求f（x）的值域；
    （3）用定义证明f（x）在（-∞，+∞）上的单调性．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．代数式sin120°cos240°的值为（　　）
    A．$-\frac{3}{4}$B．$-\frac{{\sqrt{3}}}{4}$C．$-\frac{3}{2}$D．$-\frac{1}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

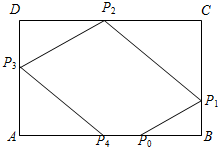    14．如图，矩形ABCD中，AB=3，AD=2，一质点从AB边上的点P0出发，沿与AB的夹角为θ的方向射到边BC上点P1后，依次反射（入射角与反射角相等）到边CD，DA和AB上的P2，P3，P4处．
    （1）若P4与P0重合，求tanθ的值；
    （2）若P4落在A、P0两点之间，且AP0=2，设tanθ=t．
    （i）求tanθ的取值范围；
    （ii）将五边形P0P1P2P3P4的面积S表示为t的函数，并求S的最大值．
    （参考结论：函数g（x）=x+$\frac{a}{x}$，（a＞0），x＞0，则函数g（x）在（0，$\sqrt{a}$]上是减函数，在[$\sqrt{a}$，+∞）是增函数．）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．设△ABC的三个内角分别为A，B，C．向量$\overrightarrow{m}$=（1，cos$\frac{C}{2}$）与$\overrightarrow{n}$=（$\sqrt{3}$sin$\frac{C}{2}$+cos$\frac{C}{2}$，$\frac{3}{2}$）共线．
    （Ⅰ）求角A，B，C的大小；
    （Ⅱ）设角A，B，C的对边分别是a，b，c，且满足2acossC+c=2b，试判断△ABC的形状．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．柳家为家里的小朋友萌萌订了一份鲜奶，牛奶公司的员工可能在早上6：30一7：30之间将鲜奶送到他家，萌萌早上上学的时间在7：00一7：40之间，则萌萌在上学前能得到鲜奶的概率为$\frac{13}{16}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．角α的终边经过点P（-1，$\sqrt{3}$），则sin（$\frac{π}{2}$+α）=-$\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．已知函数f（x）=-x2+2bx+c，任意的x1，x2∈（-∞，0）且x1≠x2时，都有$\frac{{f（{x_1}）-f（{x_2}）}}{{{x_2}-{x_1}}}$＜0，则实数b的取值范围为b≥0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．设a=3${\;}^{\frac{1}{2}}$，b=log${\;}_{\frac{1}{3}}$$\frac{1}{2}$，c=log2$\frac{1}{3}$，则a，b，c大小关系是a＞b＞c．

    查看答案和解析>>

    同步练习册答案