
【题目】已知M,N是焦点为F的抛物线y2=2px(p>0)上两个不同的点,线段MN的中点A的横坐标为![]() .
.
(1)求|MF|+|NF|的值;
(2)若p=2,直线MN与x轴交于点B,求点B的横坐标的取值范围.
【答案】(1)8;(2)![]()
【解析】
(1)根据中点坐标公式可得![]() ,利用拋物线的定义,求
,利用拋物线的定义,求![]() 的值;(2)分类讨论,设
的值;(2)分类讨论,设![]() ,利用点差法求出直线的斜率,可求点
,利用点差法求出直线的斜率,可求点![]() 横坐标为
横坐标为![]() ,再利用判别式求得
,再利用判别式求得![]() ,从而可得点
,从而可得点![]() 横坐标的取值范围.
横坐标的取值范围.
(1)设M(x1,y1),N(x2,y2),则x1+x2=8-p,而|MF|=x1+,|NF|=x2+,
∴|MF|+|NF|=x1+x2+p=8.
(2)当p=2时,抛物线方程为y2=4x.
①若直线MN的斜率不存在,则B(3,0).
②若直线MN的斜率存在,设A(3,t)(t≠0),
则由(1)知![]() 整理得
整理得![]() -
-![]() =4(x1-x2),∴
=4(x1-x2),∴![]() (y1+y2)=4,即kMN=,
(y1+y2)=4,即kMN=,
∴直线MN:y-t=(x-3),∴B点的横坐标为3-![]() ,
,
由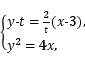 消去x得y2-2ty+2t2-12=0,由Δ>0得0<t2<12,∴3-
消去x得y2-2ty+2t2-12=0,由Δ>0得0<t2<12,∴3-![]() ∈(-3,3).
∈(-3,3).
综上,点B的横坐标的取值范围为(-3,3].


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】如图,江的两岸可近似的看成两平行的直线,江岸的一侧有A,B两个蔬菜基地,江的另一侧点C处有一个超市.已知A、B、C中任意两点间的距离为20千米.超市欲在AB之间建一个运输中转站D,A,B两处的蔬菜运抵D处后,再统一经过货轮运抵C处.由于A,B两处蔬菜的差异,这两处的运输费用也不同.如果从A处出发的运输费为每千米2元,从B处出发的运输费为每千米1元,货轮的运输费为每千米3元. 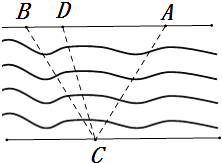
(1)设∠ADC=α,试将运输总费用S(单位:元)表示为α的函数S(α),并写出自变量的取值范围;
(2)问中转站D建在何处时,运输总费用S最小?并求出最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() (a>b>0)的左、右焦点分别是F1,F2,过F2的直线交双曲线的右支于P,Q两点,若|PF1|=|F1F2|,且3|PF2|=2|QF2|,则该双曲线的离心率为 ( )
(a>b>0)的左、右焦点分别是F1,F2,过F2的直线交双曲线的右支于P,Q两点,若|PF1|=|F1F2|,且3|PF2|=2|QF2|,则该双曲线的离心率为 ( )
A. ![]() B.
B. ![]() C. 2 D.
C. 2 D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PC⊥平面PAD,AB∥CD,CD=2AB=2BC,M,N分别是棱PA,CD的中点. 
(1)求证:PC∥平面BMN;
(2)求证:平面BMN⊥平面PAC. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,用四种不同颜色给图中的A,B,C,D,E,F六个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色,则不同的涂色方法有( )

A. 288种
B. 264种
C. 240种
D. 168种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PC⊥平面PAD,AB∥CD,CD=2AB=2BC,M,N分别是棱PA,CD的中点. 
(1)求证:PC∥平面BMN;
(2)求证:平面BMN⊥平面PAC. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊人常用小石子在沙滩上摆成各种形状来研究数,例如:

他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似地,称图2中的1,4,9,16,…这样的数为正方形数.下列数中既是三角形数又是正方形数的是
A. 289 B. 1 024 C. 1 225 D. 1 378
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高中生在被问及“家,朋友聚集的地方,个人空间”三个场所中“感到最幸福的场所在哪里?”这个问题时,从中国某城市的高中生中,随机抽取了55人,从美国某城市的高中生中随机抽取了45人进行答题.中国高中生答题情况是:选择家的占![]() 、朋友聚集的地方占
、朋友聚集的地方占![]() 、个人空间占
、个人空间占![]() .美国高中生答题情况是:朋友聚集的地方占
.美国高中生答题情况是:朋友聚集的地方占![]() 、家占
、家占![]() 、个人空间占
、个人空间占![]() .如下表:
.如下表:
在家里最幸福 | 在其它场所幸福 | 合计 | |
中国高中生 | |||
美国高中生 | |||
合计 |
(Ⅰ)请将![]() 列联表补充完整;试判断能否有
列联表补充完整;试判断能否有![]() 的把握认为“恋家”与否与国别有关;
的把握认为“恋家”与否与国别有关;
(Ⅱ)从被调查的不“恋家”的美国学生中,用分层抽样的方法选出4人接受进一步调查,再从4人中随机抽取2人到中国交流学习,求2人中含有在“个人空间”感到幸福的学生的概率.
附:![]() ,其中
,其中![]() .
.
| 0.050 | 0.025 | 0.010 | 0.001 |
| 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com