
【题目】已知函数![]()
(1)若函数![]() 的图象经过P(3,4)点,求a的值;
的图象经过P(3,4)点,求a的值;
(2)比较![]() 大小,并写出比较过程;
大小,并写出比较过程;
(3)若![]() ,求a的值.
,求a的值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】线段AB的两端在直二面角α-l-β的两个面内,并与这两个面都成30°角,则异面直线AB与l所成的角是( )
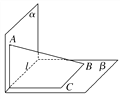
A. 30° B. 45°
C. 60° D. 75°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义满足“如果a∈A,b∈A,那么a±b∈A,且ab∈A,且![]() ∈A(b≠0)”的集合A为“闭集”.试问数集N,Z,Q,R是否分别为“闭集”?若是,请说明理由;若不是,请举反例说明.
∈A(b≠0)”的集合A为“闭集”.试问数集N,Z,Q,R是否分别为“闭集”?若是,请说明理由;若不是,请举反例说明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图![]() ,在直角梯形
,在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 是
是![]() 边的中点,将
边的中点,将![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,连接
,连接![]() ,
, ![]() ,
, ![]() ,得到如图
,得到如图![]() 所示的几何体.
所示的几何体.
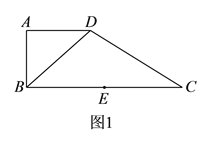
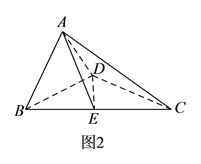
(Ⅰ)求证: ![]() 平面
平面![]() .
.
(Ⅱ)若![]() ,
, ![]() 与其在平面
与其在平面![]() 内的正投影所成角的正切值为
内的正投影所成角的正切值为![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4;坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点, ![]() 轴正半轴为极轴的极坐标中,曲线
轴正半轴为极轴的极坐标中,曲线![]() .
.
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程.
的直角坐标方程.
(Ⅱ)求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
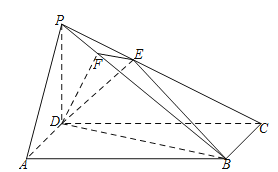
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是长方形,侧棱
是长方形,侧棱![]() 底面
底面![]() ,且
,且![]() ,过D作
,过D作![]() 于F,过F作
于F,过F作![]() 交 PC于E.
交 PC于E.
(Ⅰ)证明:![]() 平面PBC;
平面PBC;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成二面角的余弦值.
所成二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为推动乒乓球运动的发展,某乒乓球比赛允许不同协会的运动员组队参加.现有来自甲协会的运动员![]() 名,其中种子选手
名,其中种子选手![]() 名;乙协会的运动员
名;乙协会的运动员![]() 名,其中种子选手
名,其中种子选手![]() 名.从这
名.从这![]() 名运动员中随机选择
名运动员中随机选择![]() 人参加比赛.
人参加比赛.
(1)设![]() 为事件“选出的
为事件“选出的![]() 人中恰有
人中恰有![]() 名种子选手,且这
名种子选手,且这![]() 名种子选手来自同一个协会”求事件
名种子选手来自同一个协会”求事件![]() 发生的概率;
发生的概率;
(2)设![]() 为选出的
为选出的![]() 人中种子选手的人数,求随机变量
人中种子选手的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com