
【题目】如图,在直三棱柱![]() 中,
中, ![]() 是等腰直角三角形,
是等腰直角三角形, ![]() ,侧棱
,侧棱![]() ,
, ![]() 分别为
分别为![]() 与
与![]() 的中点,点
的中点,点![]() 在平面
在平面![]() 上的射影是
上的射影是![]() 的重心.
的重心.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.

【答案】(1)见解析(2)![]()
【解析】试题分析:(1)求证直线DE平行于平面ABC,可利用线面平行的判定定理,因此想到在平面ABC内找到一条与DE平行的直线即可,根据E为A1B的中点,所以可取AB的中点F,根据三角形中位线知识证出四边形DEFC为平行四边形,从而得到DE∥CF,则问题得证;
(2)连接DF,在平面EFD内过E作EH⊥DF于H,通过证明AB垂直于平面EFD得到AB⊥EH,从而说明EH垂直于平面ABD,得到∠EBH为A1B与平面ABD所成角,在直角三角形EHB中可求该角的正弦值.
试题解析:
(1)证明:如图,取AB中点F,连接EF,FC,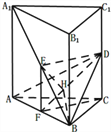
又因为E为![]() 的中点,所以EF∥
的中点,所以EF∥![]() A,EF=12
A,EF=12![]() A,又DC∥
A,又DC∥![]() A,DC=12
A,DC=12![]() A
A
所以四边形DEFC为平行四边形则ED∥CF,
因为 ![]() 是等腰直角三角形,
是等腰直角三角形, ![]() ,所以CF垂直于AB,又CF垂直于A
,所以CF垂直于AB,又CF垂直于A![]() ,
,
所以CF![]() 面
面![]() ,所以ED
,所以ED![]() 面
面![]() .
.
(2)取![]() 中点
中点![]() ,连
,连![]() ,在
,在![]() 内作
内作![]() 于点
于点![]() ,
,
由相似三角形知识求出![]()
![]()
![]() ,
, ![]() ,
, ![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,某观测站在港口A的南偏西40°方向的C处,测得一船在距观测站31海里的B处,正沿着从港口出发的一条南偏东20°的航线上向港口A开去,当船走了20海里到达D处,此时观测站又测得CD等于21海里,问此时船离港口A处还有多远? 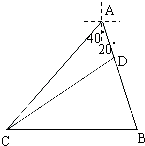
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家电公司销售部门共有200位销售员,每位部门对每位销售员都有1400万元的年度销售任务,已知这200位销售员去年完成销售额都在区间![]() (单位:百万元)内,现将其分成5组,第1组,第2组,第3组,第4组,第5组对应的区间分别为
(单位:百万元)内,现将其分成5组,第1组,第2组,第3组,第4组,第5组对应的区间分别为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,绘制出频率分布直方图.
,绘制出频率分布直方图.

(1)求![]() 的值,并计算完成年度任务的人数;
的值,并计算完成年度任务的人数;
(2)用分层抽样从这200位销售员中抽取容量为25的样本,求这5组分别应抽取的人数;
(3)现从(2)中完成年度任务的销售员中随机选取2位,奖励海南三亚三日游,求获得此奖励的2位销售员在同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn=﹣3n2+49n.
(1)请问数列{an}是否为等差数列?如果是,请证明;
(2)设bn=|an|,求数列{bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2.∠ABC=∠DBC=120°,E、F分别为AC、DC的中点. 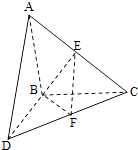
(1)求证:EF⊥BC;
(2)求二面角E﹣BF﹣C的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(3,﹣4),
=(3,﹣4), ![]() =(6,﹣3),
=(6,﹣3), ![]() =(5﹣m,﹣(3+m)).
=(5﹣m,﹣(3+m)).
(1)若点A,B,C能构成三角形,求实数m应满足的条件;
(2)若△ABC为直角三角形,且∠A为直角,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A,ω>0,﹣π<φ<π)在一个周期内的图象如图所示. 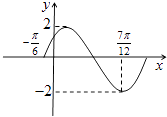
(1)求f(x)的表达式;
(2)在△ABC中,f(C+ ![]() )=﹣1且
)=﹣1且 ![]() <0,求角C.
<0,求角C.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com