
【题目】椭圆![]() 的右焦点为
的右焦点为![]() ,左顶点为
,左顶点为![]() ,线段
,线段![]() 的中点为
的中点为![]() ,圆
,圆![]() 过点
过点![]() ,且与
,且与![]() 交于
交于![]() ,
, ![]() 是等腰直角三角形,则圆
是等腰直角三角形,则圆![]() 的标准方程是____________
的标准方程是____________
【答案】![]()
【解析】
设A(﹣a,0),求得AF的中点B的坐标,可得圆F的半径和方程,设D(m,n),(m>0,n>0),E(m,﹣n),由△BDE为等腰直角三角形,可得m,n的关系,将D的坐标代入圆的方程,解方程可得m=1,求出n,代入椭圆方程,解方程可得a=2,即可得到圆F的方程.
如图设A(﹣a,0),可得a>1,c=1,b2=a2﹣1,
线段AF的中点为B(![]() ,0),
,0),
圆F的圆心为F(1,0),半径r=|BF|![]() ,
,
设D(m,n),(m>0,n>0),E(m,﹣n),
由△BDE为等腰直角三角形,可得kBD=1,
即![]() 1,即n=m
1,即n=m![]() ,
,
由D在圆F:(x﹣1)2+y2=(![]() )2上,
)2上,
可得(m﹣1)2+(m![]() )2=(
)2=(![]() )2,
)2,
化简可得(m﹣1)(2m﹣1+a)=0,
解得m=1或m![]() (舍去),
(舍去),
则n![]() ,
,
将D(1,![]() )代入椭圆方程,可得
)代入椭圆方程,可得
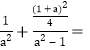 1,
1,
化简可得a=2或![]() (舍去),
(舍去),
则圆F的标准方程为(x﹣1)2+y2![]() ,
,
故答案为:(x﹣1)2+y2![]() .
.


科目:高中数学 来源: 题型:
【题目】给出下列结论:
①若![]() 为真命题,则
为真命题,则![]() 、
、![]() 均为真命题;
均为真命题;
②命题“若![]() ,则
,则![]() ”的逆否命题是“若
”的逆否命题是“若![]() ,则
,则![]() ”;
”;
③若命题![]() ,
,![]() ,则
,则![]() ,
,![]() ;
;
④“![]() ”是“
”是“![]() ”的充分不必要条件.其中正确的结论有____.
”的充分不必要条件.其中正确的结论有____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中有四个小球,分别写有“美、丽、中、国”四个字,有放回地从中任取一个小球,直到“中”“国”两个字都取到就停止,用随机模拟的方法估计恰好在第三次停止的概率.利用电脑随机产生0到3之间取整数值的随机数,分别用0,1,2,3代表“中、国、美、丽”这四个字,以每三个随机数为一组,表示取球三次的结果,经随机模拟产生了以下18组随机数:
232 321 230 023 123 021 132 220 001
231 130 133 231 031 320 122 103 233
由此可以估计,恰好第三次就停止的概率为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)在线段![]() 上,是否存在一点
上,是否存在一点![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() ?如果存在,求
?如果存在,求![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】部分与整体以某种相似的方式呈现称为分形.谢尔宾斯基三角形是一种分形,由波兰数学家谢尔宾斯基1915年提出.具体操作是取一个实心三角形,沿三角形的三边中点连线,将它分成4个小三角形,去掉中间的那一个小三角形后,对其余3个小三角形重复上述过程逐次得到各个图形,如图.

现在上述图(3)中随机选取一个点,则此点取自阴影部分的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:区间![]() ,
,![]() ,
,![]() ,
,![]() 的长度均为
的长度均为![]() ,若不等式
,若不等式![]() 的解集是互不相交区间的并集,设该不等式的解集中所有区间的长度之和为
的解集是互不相交区间的并集,设该不等式的解集中所有区间的长度之和为![]() ,则( )
,则( )
A. 当![]() 时,
时,![]() B. 当
B. 当![]() 时,
时,![]()
C. 当![]() 时,
时,![]() D. 当
D. 当![]() 时,
时,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中所有正确的序号是_________
①两直线的倾斜角相等,则斜率必相等;
②若动点![]() 到定点
到定点![]() 和定直线
和定直线![]() 的距离相等,则动点
的距离相等,则动点![]() 的轨迹是抛物线;
的轨迹是抛物线;
③已知![]() 、
、![]() 是椭圆
是椭圆![]() 的两个焦点,过点
的两个焦点,过点![]() 的直线与椭圆交于
的直线与椭圆交于![]() 、
、![]() 两点,则
两点,则![]() 的周长为
的周长为![]() ;
;
④曲线的参数方程为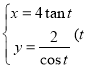 为参数
为参数![]() ,则它表示双曲线且渐近线方程为
,则它表示双曲线且渐近线方程为![]() ;
;
⑤已知正方形![]() ,则以
,则以![]() 、
、![]() 为焦点,且过
为焦点,且过![]() 、
、![]() 两点的椭圆的离心率为
两点的椭圆的离心率为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知P是矩形ABCD所在平面上的一点,则有![]() .试证明该命题.
.试证明该命题.
(2)将上述命题推广到P为空间上任一点的情形,写出这个推广后的命题并加以证明.
(3)将矩形ABCD进一步推广到长方体![]() ,并利用(2)得到的命题建立并证明一个新命题.
,并利用(2)得到的命题建立并证明一个新命题.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com