[题目]已知动点到点的距离比它到直线的距离小 .记动点的轨迹为 .若以为圆心. 为半径( )作圆.分别交轴于两点.连结并延长 .分别交曲线于两点.(1)求曲线的方程,(2)求证:直线的斜率为定值. 题目和参考答案——青夏教育精英家教网—

【题目】已知动点到点的距离比它到直线的距离小，记动点的轨迹为 .若以为圆心，为半径（）作圆，分别交轴于两点，连结并延长，分别交曲线于两点.
（1）求曲线的方程；
（2）求证：直线的斜率为定值.

【答案】
（1）解：动点到点的距离比它到直线的距离小，可得动点到点的距离与它到直线的距离相等，由定义可得曲线方程为
（2）解：设，与抛物线方程联立得：，
由题意有，
【解析】本题考查抛物线方程的求法，考查两直线的斜率的比值是否为定值的判断与求法，解题时要认真审题，注意直线方程的合理运用．
【考点精析】认真审题，首先需要了解抛物线的定义(平面内与一个定点和一条定直线的距离相等的点的轨迹称为抛物线．定点称为抛物线的焦点，定直线称为抛物线的准线)．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知椭圆的两个焦点为F1（﹣ ，0），F2（，0），M是椭圆上一点，若 =0，| || |=8．
（1）求椭圆的方程；
（2）点P是椭圆上任意一点，A1、A2分别是椭圆的左、右顶点，直线PA1 ， PA2与直线x= 分别交于E，F两点，试证：以EF为直径的圆交x轴于定点，并求该定点的坐标．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】为了引导居民合理用水，某市决定全面实施阶梯水价，阶梯水价原则上以住宅（一套住宅为一户）的月用水量为基准定价，具体划分标准如表：

阶梯级别	第一阶梯水量	第二阶梯水量	第三阶梯水量
月用水量范围（单位：立方米）	（0，10]	（10，15]	（15，+∞）

从本市随机抽取了10户家庭，统计了同一个月的用水量，得到如图所示的茎叶图．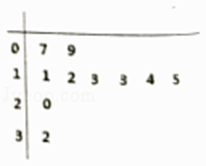

（1）现要在这10户家庭中任意选取3户，求取到第二阶梯水量的户数的分布列和均值；
（2）用抽到的10户家庭作为样本估计全市的居民用水情况，从全市依次随机抽取10户，若抽到n户月用水量为第二阶梯水量的可能性最大，求出n的值．