
分析 由条件利用同角三角函数的基本关系,两角差的正弦公式,求得$sin(A+\frac{π}{4})$的值.
解答 解:△ABC中,$cosA=\frac{4}{5}$,∴sinA=$\frac{3}{5}$,则$sin(A+\frac{π}{4})$=sinAcos$\frac{π}{4}$+cosAsin$\frac{π}{4}$=$\frac{3}{5}•\frac{\sqrt{2}}{2}$+$\frac{4}{5}•\frac{\sqrt{2}}{2}$=$\frac{7\sqrt{2}}{10}$,
故答案为:$\frac{7\sqrt{2}}{10}$.
点评 本题主要考查同角三角函数的基本关系,两角差的正弦公式的应用,属于基础题.


 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
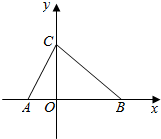 如图,在平面直角坐标系xOy中,∠CAB=60°,AC=4,BC=2$\sqrt{7}$
如图,在平面直角坐标系xOy中,∠CAB=60°,AC=4,BC=2$\sqrt{7}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 67°30′化成弧度是$\frac{3}{8}$π | B. | -$\frac{10}{3}$π化成度是-600° | ||
| C. | -150°化成弧度是$\frac{5}{6}$π | D. | $\frac{π}{12}$化成度是15° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com