
【题目】已知圆锥曲线 E: ![]() .
.
(I)求曲线 E的离心率及标准方程;
(II)设 M(x0 , y0)是曲线 E上的任意一点,过原点作⊙M:(x﹣x0)2+(y﹣y0)2=8的两条切线,分别交曲线 E于点 P、Q.
①若直线OP,OQ的斜率存在分别为k1 , k2 , 求证:k1k2=﹣ ![]() ;
;
②试问OP2+OQ2是否为定值.若是求出这个定值,若不是请说明理由.
【答案】解:(I)由椭圆定义可知,曲线E是以 ![]() 和
和 ![]() 为焦点,长轴长为
为焦点,长轴长为 ![]() 的椭圆,
的椭圆,
设椭圆的半长轴长、半短轴长、半焦距分别为a、b、c.
∴ ![]() ,
, ![]() ,则
,则 ![]() ,
,
∴椭圆的离心率 ![]() ,E的标准方程为
,E的标准方程为 ![]() .
.
(II)①证明:若过原点与⊙M相切的直线斜率存在设为k,
则切线方程为y=kx,∴ ![]() ,
,
整理得 ![]() .
.
由题设可知k1 , k2是以上关于k的一元二次方程的两个实根,
∴ 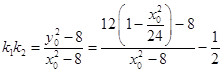 ,即
,即 ![]() .
.
②设 P(x1 , y1),Q(x2 , y2).
当直线 O P,OQ的斜率存在时,
由①易得 ![]() ,
, ![]() ,
,
而 ![]() =
= ![]() =
= ![]() =
= 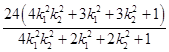 =
= 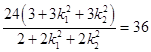
当直线 O P或 OQ的斜率不存在时,圆 M与y轴相切,且圆 M也与x轴相切 P,Q是椭圆 E的两个顶点,∴O P2+OQ2=a2+b2=36.
综上所述:O P2+OQ2为定值36.
【解析】(I)由椭圆定义可知,曲线E是以 ![]() 和
和 ![]() 为焦点,长轴长为
为焦点,长轴长为 ![]() 的椭圆,即可得出.(II)①若过原点与⊙M相切的直线斜率存在设为k,则切线方程为y=kx,可得
的椭圆,即可得出.(II)①若过原点与⊙M相切的直线斜率存在设为k,则切线方程为y=kx,可得 ![]() ,整理得
,整理得 ![]() .由题设可知k1 , k2是以上关于k的一元二次方程的两个实根,利用根与系数的关系即可得出.②设 P(x1 , y1),Q(x2 , y2).当直线 O P,OQ的斜率存在时,由①易得
.由题设可知k1 , k2是以上关于k的一元二次方程的两个实根,利用根与系数的关系即可得出.②设 P(x1 , y1),Q(x2 , y2).当直线 O P,OQ的斜率存在时,由①易得 ![]() ,
, ![]() ,利用两点之间的距离、根与系数的关系即可得出.当直线 O P,OQ的斜率不存在时直接验证即可得出.
,利用两点之间的距离、根与系数的关系即可得出.当直线 O P,OQ的斜率不存在时直接验证即可得出.


科目:高中数学 来源: 题型:
【题目】下列命题正确的序号为______.
①周期函数都有最小正周期;②偶函数一定不存在反函数;
③“![]() 是单调函数”是“
是单调函数”是“![]() 存在反函数”的充分不必要条件;
存在反函数”的充分不必要条件;
④若原函数与反函数的图像有偶数个交点,则可能都不在直线![]() 上;
上;
查看答案和解析>>
科目:高中数学 来源: 题型:
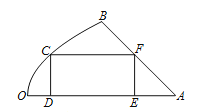
【题目】如图是一块地皮![]() ,其中
,其中![]() ,
, ![]() 是直线段,曲线段
是直线段,曲线段![]() 是抛物线的一部分,且点
是抛物线的一部分,且点![]() 是该抛物线的顶点,
是该抛物线的顶点, ![]() 所在的直线是该抛物线的对称轴.经测量,
所在的直线是该抛物线的对称轴.经测量, ![]() km,
km, ![]() km,
km, ![]() .现要从这块地皮中划一个矩形
.现要从这块地皮中划一个矩形![]() 来建造草坪,其中点
来建造草坪,其中点![]() 在曲线段
在曲线段![]() 上,点
上,点![]() ,
, ![]() 在直线段
在直线段![]() 上,点
上,点![]() 在直线段
在直线段![]() 上,设
上,设![]() km,矩形草坪
km,矩形草坪![]() 的面积为
的面积为![]() km2.
km2.
(1)求![]() ,并写出定义域;
,并写出定义域;
(2)当![]() 为多少时,矩形草坪
为多少时,矩形草坪![]() 的面积最大?
的面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义在![]() 上的函数
上的函数![]() 满足:对任意的
满足:对任意的![]() ,当
,当![]() 时,都有
时,都有![]() ,则称
,则称![]() 是“非減函数”.
是“非減函数”.
(1)若![]() 是“非減函数”,求
是“非減函数”,求![]() 的取值范围;
的取值范围;
(2)若![]() 为周期函数,且为“非减函数”,证明
为周期函数,且为“非减函数”,证明![]() 是常值函数;
是常值函数;
(3)设![]() 恒大于零,
恒大于零,![]() 是定义在R上、恒大于零的周期函数,
是定义在R上、恒大于零的周期函数,![]() 是
是![]() 的最大值。函数
的最大值。函数![]() 。证明:“
。证明:“![]() 是周期函数”的充要条件“
是周期函数”的充要条件“![]() 是常值函数”.
是常值函数”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学城校区与本部校区之间的驾车单程所需时间为![]() ,
,![]() 只与道路畅通状况有关,对其容量为500的样本进行统计,结果如下:
只与道路畅通状况有关,对其容量为500的样本进行统计,结果如下:
| 25 | 30 | 35 | 40 |
频数(次) | 100 | 150 | 200 | 50 |
以这500次驾车单程所需时间的频率代替某人1次驾车单程所需时间的概率.
(1)求![]() 的分布列与
的分布列与![]() ;
;
(2)某天有3位教师独自驾车从大学城校区返回本部校区,记![]() 表示这3位教师中驾车所用时间少于
表示这3位教师中驾车所用时间少于![]() 的人数,求
的人数,求![]() 的分布列与
的分布列与![]() ;
;
(3)下周某天张老师将驾车从大学城校区出发,前往本部校区做一个50分钟的讲座,结束后立即返回大学城校区,求张老师从离开大学城校区到返回大学城校区共用时间不超过120分钟的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn=k3n﹣m,且a1=3,a3=27.
(I)求证:数列{an}是等比数列;
(II)若anbn=log3an+1 , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,其中左焦点
,其中左焦点![]() (-2,0).
(-2,0).
(1) 求椭圆C的方程;
(2) 若直线y=x+m与椭圆C交于不同的两点A,B,且线段AB的中点M在圆x2+y2=1上,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1: ![]() =1(a>b>0)的离心率为e=
=1(a>b>0)的离心率为e= ![]() ,且过点(1,
,且过点(1, ![]() ).抛物线C2:x2=﹣2py(p>0)的焦点坐标为(0,﹣
).抛物线C2:x2=﹣2py(p>0)的焦点坐标为(0,﹣ ![]() ).
).
(Ⅰ)求椭圆C1和抛物线C2的方程;
(Ⅱ)若点M是直线l:2x﹣4y+3=0上的动点,过点M作抛物线C2的两条切线,切点分别为A,B,直线AB交椭圆C1于P,Q两点.
(i)求证直线AB过定点,并求出该定点坐标;
(ii)当△OPQ的面积取最大值时,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=![]() (a∈R).
(a∈R).
(1)若f(x)在x=0处取得极值,确定a的值,并求此时曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若f(x)在[3,+∞)上为减函数,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com