
已知函数f(x)=ex-e-x(x∈R且e为自然对数的底数).
(1)判断函数f(x)的奇偶性与单调性;
(2)是否存在实数t,使不等式f(x-t)+f(x2-t2)≥0对一切x都成立?若存在,求出t;若不存在,请说明理由.
(1) f(x)是奇函数 (2) 存在实数t=-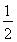 ,使不等式f(x-t)+f(x2-t2)≥0对一切x都成立
,使不等式f(x-t)+f(x2-t2)≥0对一切x都成立
【解析】(1)∵f(x)=ex-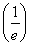 x,且y=ex是增函数,
x,且y=ex是增函数,
y=-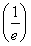 x是增函数,∴f(x)是增函数.
x是增函数,∴f(x)是增函数.
由于f(x)的定义域为R,且f(-x)=e-x-ex=-f(x),
∴f(x)是奇函数.
(2)由(1)知f(x)是增函数和奇函数,
∴f(x-t)+f(x2-t2)≥0对一切x∈R恒成立
?f(x2-t2)≥f(t-x)对一切x∈R恒成立
?x2-t2≥t-x对一切x∈R恒成立
?t2+t≤x2+x对一切x∈R恒成立
?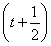 2≤
2≤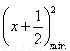 对一切x∈R恒成立
对一切x∈R恒成立
?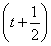 2≤0?t=-
2≤0?t=-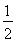 .
.
即存在实数t=-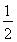 ,使不等式f(x-t)+f(x2-t2)≥0对一切x都成立.
,使不等式f(x-t)+f(x2-t2)≥0对一切x都成立.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第3课时练习卷(解析版) 题型:选择题
下面是关于复数z=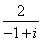 的四个命题:
的四个命题:
p1:|z|=2,p2:z2=2i,
p3:z的共轭复数为1+i,p4:z的虚部为-1.
其中的真命题为( )
A.p1,p3 B.p1,p2
C.p2,p4 D.p3,p4
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第5课时练习卷(解析版) 题型:选择题
设函数f(x)的定义域为R,x0(x0≠0)是f(x)的极大值点,以下结论一定正确的是( )
A.?x∈R,f(x)≤f(x0)
B.-x0是f(-x)的极小值点
C.-x0是-f(x)的极小值点
D.-x0是-f(-x)的极小值点
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第3课时练习卷(解析版) 题型:解答题
设f(x)=|lg x|,a,b为实数,且0<a<b.
(1)求方程f(x)=1的解;
(2)若a,b满足f(a)=f(b)=2f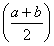 ,
,
求证:a·b=1,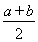 >1.
>1.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第3课时练习卷(解析版) 题型:选择题
如果一个点是一个指数函数和一个对数函数的图象的交点,那么称这个点为“好点”.下列四个点P1(1,1),P2(1,2),P3 ,P4(2,2)中,“好点”的个数为( )
,P4(2,2)中,“好点”的个数为( )
A.1 B.2
C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第2课时练习卷(解析版) 题型:选择题
已知函数f(x)=x2-2(a+2)x+a2,g(x)=-x2+2(a-2)x-a2+8.设H1(x)=max{f(x),g(x)},H2(x)=min{f(x),g(x)}(max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记H1(x)的最小值为A,H2(x)的最大值为B,则A-B=( )
A.16 B.-16
C.a2-2a-16 D.a2+2a-16
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第1课时练习卷(解析版) 题型:填空题
已知在实数a,b满足某一前提条件时,命题“若a>b,则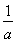 <
<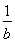 ”及其逆命题、否命题和逆否命题都是假命题,则实数a,b应满足的前提条件是________.
”及其逆命题、否命题和逆否命题都是假命题,则实数a,b应满足的前提条件是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题四练习卷(解析版) 题型:解答题
已知n∈N*,数列{dn}满足dn=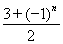 ,数列{an}满足an=d1+d2+d3+…+d2n.又知数列{bn}中,b1=2,且对任意正整数m,n,
,数列{an}满足an=d1+d2+d3+…+d2n.又知数列{bn}中,b1=2,且对任意正整数m,n,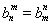 .
.
(1)求数列{an}和数列{bn}的通项公式;
(2)将数列{bn}中的第a1项,第a2项,第a3项,…,第an项删去后,剩余的项按从小到大的顺序排成新数列{cn},求数列{cn}的前2013项和T2013.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题八练习卷(解析版) 题型:选择题
已知函数f(x)= 若函数g(x)=f(x)-m有三个不同的零点,则实数m的取值范围为( )
若函数g(x)=f(x)-m有三个不同的零点,则实数m的取值范围为( )
A.-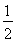 ,1 B.-
,1 B.-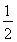 ,1 C.-
,1 C.-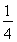 ,0 D.-
,0 D.- ,0
,0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com