
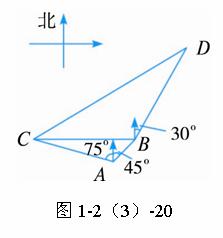
思路分析:设经过t小时后,缉私船能最快追上走私船,即在图中的D处恰好两船相遇,CD方向即是缉私船的追截方向,利用正、余弦定理根据条件解三角形.
解:设缉私船追上走私船所需的时间为t小时,则CD=10![]() t,BD=10t.
t,BD=10t.
在△ABC中,∵AB=![]() -1,AC=2,∠BAC=45°+75°=120°,
-1,AC=2,∠BAC=45°+75°=120°,
由余弦定理,得BC=![]() =
=![]() .
.
由正弦定理,得sin∠ABC=![]() =
=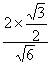
![]() .
.
∴∠ABC=45°,易知CB方向与正北方向垂直,则∠CBD=90°+30°=120°.
在△BCD中,由正弦定理,得sin∠BCD=![]() =
=![]() =
=![]() .
.
∴∠BCD=30°,∠BDC=30°.
∴BD=BC=![]() .
.
∴10t=6,即t=![]() .
.
∴缉私船沿北偏东60°方向能最快追上走私船,需要![]() 小时.
小时.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
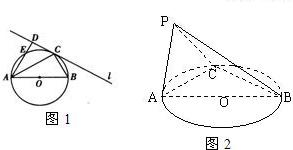 如图1所示,圆O的直径AB=6,C为圆周上一点,BC=3.过C作圆的切线l,过A作l的垂线AD,AD与直线l、圆O分别交于点D、E.
如图1所示,圆O的直径AB=6,C为圆周上一点,BC=3.过C作圆的切线l,过A作l的垂线AD,AD与直线l、圆O分别交于点D、E.查看答案和解析>>
科目:高中数学 来源: 题型:
 (1)现有一个破损的圆块(如图1),只给出一把带有刻度的直尺和一个量角器,请你设计一种方案,求出这个圆块的直径的长度.
(1)现有一个破损的圆块(如图1),只给出一把带有刻度的直尺和一个量角器,请你设计一种方案,求出这个圆块的直径的长度.查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 32 |
| 1 |
| 33 |
| 1 |
| 312 |
| 1 |
| 32 |
| 1 |
| 33 |
| 1 |
| 312 |

查看答案和解析>>
科目:高中数学 来源: 题型:
 函数y=f(x),定义域为(-
函数y=f(x),定义域为(-| 3 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:

图1-2-13
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com