
分析 ①设出对称点的坐标,根据垂直的条件和中点坐标公式,列出方程组,求出实数解即可;
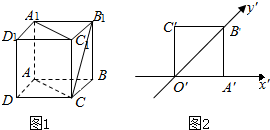
②根据正方体的对角线即为外接球的直径,即可判断;
③由异面直线所成的角的定义,先找(作)平行线,再解三角形,即可求得;
④根据水平放置的平面图形的直观图的画法:平行性质不变,长度是与x轴平行的不变,与y轴平行的是原来的一半.即可画出原图形.
解答 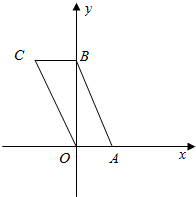 解:①设点A(1,2)关于直线y=x-1的对称点B的坐标为(m,n),
解:①设点A(1,2)关于直线y=x-1的对称点B的坐标为(m,n),
则$\left\{\begin{array}{l}{\frac{1}{2}(m+1)-1=\frac{1}{2}(n+2)}\\{n-2=-(m-1)}\end{array}\right.$,解得,m=3,n=0,故①正确;
②已知正方体的棱长等于2,那么正方体外接球的直径为2$\sqrt{3}$,故半径是$\sqrt{3}$,即③错;
③正方体ABCD-A1B1C1D1中,可得A1D∥B1C,∠C1A1D为异面直线A1C1与B1C成的角,在等边△A1DC1中,∠C1A1D=60°,
故异面直线A1C1与B1C成60°的角,即③正确;
④由水平放置的一个平面图形的直观图的画法,得到原图形为平行四边形,如图,故④错.
故答案为:①③.
点评 本题考查命题的真假判断与应用,考查了点关于直线的对称点的求法、正方体与其外接球的关系,以及空间异面直线所成的角和水平放置的平面图的直观图的画法,掌握这些基础知识是迅速解题的关键,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{10}}{2}$ | B. | $\sqrt{10}$ | C. | $\frac{\sqrt{35}}{2}$ | D. | $\sqrt{35}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sin1>sin1.2>sin1.5 | B. | sin1>sin1.5>sin1.2 | ||
| C. | sin1.5>sin1.2>sin1 | D. | sin1.2>sin1>sin1.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\sqrt{5}$ | B. | -$\frac{\sqrt{6}}{2}$ | C. | -$\sqrt{6}$ | D. | -$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com