
【题目】如图,四边形ABCD为菱形,四边形ACEF为平行四边形,设BD与AC相交于点G,AB=BD=2,AE= ![]() ,∠EAD=∠EAB.
,∠EAD=∠EAB. 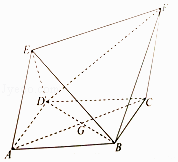
(1)证明:平面ACEF⊥平面ABCD;
(2)若AE与平面ABCD所成角为60°,求二面角B﹣EF﹣D的余弦值.
【答案】
(1)证明:连接EG,
∵四边形ABCD为菱形,∴AD=AB,BD⊥AC,DG=GB,
在△EAD和△EAB中,
AD=AB,AE=AE,∠EAD=∠EAB,
∴△EAD≌△EAB,
∴ED=EB,则BD⊥EG,
又AC∩EG=G,∴BD⊥平面ACEF,
∵BD平面ABCD,
∴平面ACEF⊥平面ABCD
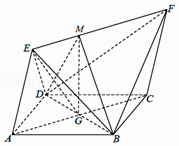
(2)解法一:过G作EF的垂线,垂足为M,连接MB,MG,MD,
易得∠EAC为AE与面ABCD所成的角,
∴∠EAC=60°,
∵EF⊥GM,EF⊥BD,
∴EF⊥平面BDM,
∴∠DMB为二面角B﹣EF﹣D的平面角,
可求得MG= ![]() ,DM=BM=
,DM=BM= ![]() ,
,
在△DMB中,由余弦定理可得:cos∠BMD= ![]() ,
,
∴二面角B﹣EF﹣D的余弦值为 ![]() ;
;
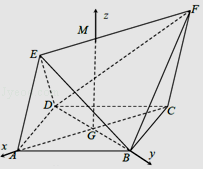
解法二:如图,在平面ABCD内,过G作AC的垂线,交EF于M点,
由(1)可知,平面ACEF⊥平面ABCD,
∵MG⊥平面ABCD,
∴直线GM、GA、GB两两互相垂直,
分别以GA、GB、GM为x、y、z轴建立空间直角坐标系G﹣xyz,
可得∠EAC为AE与平面ABCD所成的角,∴∠EAC=60°,
则D(0,﹣1,0),B(0,1,0),E( ![]() ),F(
),F( ![]() ),
),
![]() ,
, ![]() ,
,
设平面BEF的一个法向量为 ![]() ,则
,则
 ,
,
取z=2,可得平面BEF的一个法向量为 ![]() ,
,
同理可求得平面DEF的一个法向量为 ![]() ,
,
∴cos< ![]() >=
>= ![]() =
= ![]() ,
,
∴二面角B﹣EF﹣D的余弦值为 ![]() .
.
【解析】(1)连接EG,由四边形ABCD为菱形,可得AD=AB,BD⊥AC,DG=GB,可证△EAD≌△EAB,进一步证明BD⊥平面ACEF,则平面ACEF⊥平面ABCD;(2)法一、过G作EF的垂线,垂足为M,连接MB,MG,MD,可得∠EAC为AE与面ABCD所成的角,得到EF⊥平面BDM,可得∠DMB为二面角B﹣EF﹣D的平面角, 在△DMB中,由余弦定理求得∠BMD的余弦值,进一步得到二面角B﹣EF﹣D的余弦值;
法二、在平面ABCD内,过G作AC的垂线,交EF于M点,由(1)可知,平面ACEF⊥平面ABCD,得MG⊥平面ABCD,则直线GM、GA、GB两两互相垂直,分别以GA、GB、GM为x、y、z轴建立空间直角坐标系G﹣xyz,分别求出平面BEF与平面DEF的一个法向量,由两法向量所成角的余弦值可得二面角B﹣EF﹣D的余弦值.


科目:高中数学 来源: 题型:
【题目】近年来,郑州经济快速发展,跻身新一线城市行列,备受全国瞩目.无论是市内的井字形快速交通网,还是辐射全国的米字形高铁路网,郑州的交通优势在同级别的城市内无能出其右.为了调查郑州市民对出行的满意程度,研究人员随机抽取了1000名市民进行调查,并将满意程度以分数的形式统计成如下的频率分布直方图,其中![]() .
.

(I)求![]() 的值;
的值;
(Ⅱ)求被调查的市民的满意程度的平均数,众数,中位数;
(Ⅲ)若按照分层抽样从![]() ,
,![]() 中随机抽取8人,再从这8人中随机抽取2人,求至少有1人的分数在
中随机抽取8人,再从这8人中随机抽取2人,求至少有1人的分数在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,焦点到相应准线的距离为
,焦点到相应准线的距离为![]() ,
,![]() ,
,![]() 分别为椭圆的左顶点和下顶点,
分别为椭圆的左顶点和下顶点,![]() 为椭圆
为椭圆![]() 上位于第一象限内的一点,
上位于第一象限内的一点,![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() .
.
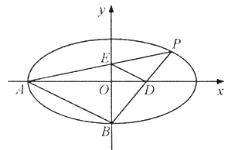
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)求证:四边形![]() 的面积为定值.
的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】不等式组 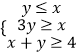 的解集记为D,命题p:(x,y)∈D,x+2y≥5,命题q:(x,y)∈D,2x﹣y<2,则下列命题为真命题的是( )
的解集记为D,命题p:(x,y)∈D,x+2y≥5,命题q:(x,y)∈D,2x﹣y<2,则下列命题为真命题的是( )
A.p
B.q
C.p∨(q)
D.(p)∨q
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接夏季旅游旺季的到来,少林寺单独设置了一个专门安排游客住宿的客栈,寺庙的工作人员发现为游客准备的一些食物有些月份剩余不少,浪费很严重,为了控制经营成本,减少浪费,就想适时调整投入.为此他们统计每个月入住的游客人数,发现每年各个月份来客栈入住的游客人数会发生周期性的变化,并且有以下规律:
①每年相同的月份,入住客栈的游客人数基本相同;
②入住客栈的游客人数在2月份最少,在8月份最多,相差约400人;
③2月份入住客栈的游客约为100人,随后逐月递增直到8月份达到最多.
(1)试用一个正弦型三角函数![]() 描述一年中入住客栈的游客人数y与月x份之间的关系;
描述一年中入住客栈的游客人数y与月x份之间的关系;
(2)请问哪几个月份要准备400份以上的食物?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心在
的圆心在![]() 轴上,且经过点
轴上,且经过点![]() ,
,![]() .
.
(Ⅰ)求线段AB的垂直平分线方程;
(Ⅱ)求圆![]() 的标准方程;
的标准方程;
(Ⅲ)过点![]() 的直线
的直线![]() 与圆
与圆![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() =1(a>b>0)的左、右焦点分别为F1、F2 , A为椭圆E的右顶点,B,C分别为椭圆E的上、下顶点.线段CF2的延长线与线段AB交于点M,与椭圆E交于点P.
=1(a>b>0)的左、右焦点分别为F1、F2 , A为椭圆E的右顶点,B,C分别为椭圆E的上、下顶点.线段CF2的延长线与线段AB交于点M,与椭圆E交于点P.
(1)若椭圆的离心率为 ![]() ,△PF1C的面积为12,求椭圆E的方程;
,△PF1C的面积为12,求椭圆E的方程;
(2)设S ![]() =λS
=λS ![]() ,求实数λ的最小值.
,求实数λ的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=sin(ωx+φ)+ ![]() 的图象过(1,2),若f(x)相邻的零点为x1 , x2且满足|x1﹣x2|=6,则f(x)的单调增区间为( )
的图象过(1,2),若f(x)相邻的零点为x1 , x2且满足|x1﹣x2|=6,则f(x)的单调增区间为( )
A.[﹣2+12k,4+12k](k∈Z)
B.[﹣5+12k,1+12k](k∈Z)
C.[1+12k,7+12k](k∈Z)
D.[﹣2+6k,1+6k](k∈Z)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com