
 如图,圆O的半径为$\sqrt{2}$,A,B为圆O上的两个定点,且∠AOB=90°,P为优弧AB的中点,设C,D(C在D左侧)为优弧AB上的两个不同的动点,且CD∥BA,记∠POD=α,四边形ABCD的面积为S.
如图,圆O的半径为$\sqrt{2}$,A,B为圆O上的两个定点,且∠AOB=90°,P为优弧AB的中点,设C,D(C在D左侧)为优弧AB上的两个不同的动点,且CD∥BA,记∠POD=α,四边形ABCD的面积为S.分析 (1)求出O到AB和CD的距离,AB与CD的长,代入梯形面积公式,可得S关于α的函数关系;
(2)结合正弦函数的图象和性质及二次函数的图象和性质,可得S的最大值及最大值点.
解答 解:(1)如下图所示: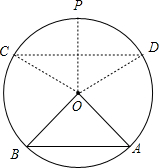
∵圆O的半径为$\sqrt{2}$,A,B为圆O上的两个定点,且∠AOB=90°,
∴AB=$\sqrt{{OB}^{2}+{OA}^{2}}$=2,O到AB的距离d=1,
若∠POD=α,则CD=2$\sqrt{2}$sinα,O到CD的距离h=$\sqrt{2}$cosα,
故S=$\frac{1}{2}$(2$\sqrt{2}$sinα+2)($\sqrt{2}$cosα+1)=2sinαcosα+$\sqrt{2}$(sinα+cosα)+1=(sinα+cosα)2+$\sqrt{2}$(sinα+cosα)=2sin2(α+$\frac{π}{4}$)+2sin(α+$\frac{π}{4}$).
(2)令t=sin(α+$\frac{π}{4}$).则S=2t2+2t,t∈[$\frac{\sqrt{2}}{2}$,1],
∵S=2t2+2t的图象是开口朝上,且以直线t=-$\frac{1}{2}$为对称的抛物线,
故当t=1,即α=$\frac{π}{4}$时,S取最大值4.
点评 本题考查的知识点是函数的解析式的求不地,函数的最值及其几何意义,二次函数的图象和性质,正弦函数的图象和性质,难度中档.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
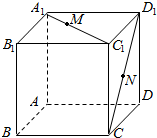 在长方体ABCD-A1B1C1D1中,|AB|=|AD|=3,|AA1|=3,点M在A1C1上,|MC1|=2|A1M|,N在D1C上且为D1C的中点,求M,N两点间的距离.
在长方体ABCD-A1B1C1D1中,|AB|=|AD|=3,|AA1|=3,点M在A1C1上,|MC1|=2|A1M|,N在D1C上且为D1C的中点,求M,N两点间的距离.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin(x+$\frac{π}{3}$) | B. | y=cos(x-$\frac{π}{3}$) | C. | y=sin(x+$\frac{π}{6}$) | D. | y=tan(x+$\frac{π}{6}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com