
【题目】三名工人加工同一种零件,他们在一天中的工作情况如图所示,其中点![]() 的横、纵坐标分别为第
的横、纵坐标分别为第![]() 名工人上午的工作时间和加工的零件数,点
名工人上午的工作时间和加工的零件数,点![]() 的横、纵坐标分别为第
的横、纵坐标分别为第![]() 名工人下午的工作时间和加工的零件数,
名工人下午的工作时间和加工的零件数,![]() .记
.记![]() 为第
为第![]() 名工人在这一天中加工的零件总数,记
名工人在这一天中加工的零件总数,记![]() 为第
为第![]() 名工人在这一天中平均加工的零件数,则
名工人在这一天中平均加工的零件数,则![]() ,
,![]() ,
,![]() 中的最大值与
中的最大值与![]() ,
,![]() ,
,![]() 中的最大值分别是( )
中的最大值分别是( )

A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】程大位是明代著名数学家,他的《新编直指算法统宗》是中国历史上一部影响巨大的著作.卷八中第33问:“今有三角果一垛,底阔每面七个.问该若干?”如图是解决该问题的程序框图.执行该程序框图,求得该垛果子的总数S为( )
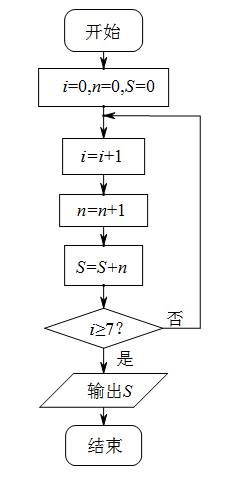
A.28B.56C.84D.120
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 年俄罗斯索契冬奥会某项目的选拔比赛中,
年俄罗斯索契冬奥会某项目的选拔比赛中,![]() 、
、![]() 两个代表队进行对抗赛,每队三名队员,
两个代表队进行对抗赛,每队三名队员,![]() 队队员是
队队员是![]() 、
、![]() 、
、![]() ,
,![]() 队队员是
队队员是![]() 、
、![]() 、
、![]() ,按以往多次比赛的统计,对阵队员之间胜负概率如下表,现按表中对阵方式出场进行三场比赛,每场胜队得
,按以往多次比赛的统计,对阵队员之间胜负概率如下表,现按表中对阵方式出场进行三场比赛,每场胜队得![]() 分,负队得
分,负队得![]() 分,设
分,设![]() 队、
队、![]() 队最后所得总分分别为
队最后所得总分分别为![]() 、
、![]() 且
且![]() .
.
对阵队员 |
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 队得分为
队得分为![]() 分的概率;
分的概率;
(2)求![]() 的分布列;并用统计学的知识说明哪个队实力较强.
的分布列;并用统计学的知识说明哪个队实力较强.
查看答案和解析>>
科目:高中数学 来源: 题型:
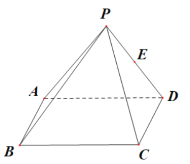
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为矩形,
为矩形,![]() ,侧面
,侧面![]() 为等边三角形且垂直于底面
为等边三角形且垂直于底面![]() ,
,![]() 是
是![]() 的中点.
的中点.
(1)在棱![]() 上取一点
上取一点![]() 使直线
使直线![]() ∥平面
∥平面![]() 并证明;
并证明;
(2)在(1)的条件下,当棱![]() 上存在一点
上存在一点![]() ,使得直线
,使得直线![]() 与底面
与底面![]() 所成角为
所成角为![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中为了了解高三学生每天自主参加体育锻炼的情况,随机抽取了100名学生进行调查,其中女生有55名.下面是根据调查结果绘制的学生自主参加体育锻炼时间的频率分布直方图:
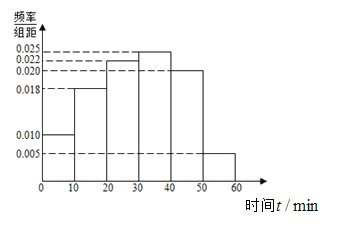
将每天自主参加体育锻炼时间不低于40分钟的学生称为体育健康A类学生,已知体育健康A类学生中有10名女生.
(Ⅰ)根据已知条件完成下面![]() 列联表,并据此资料你是否认为达到体育健康A类学生与性别有关?
列联表,并据此资料你是否认为达到体育健康A类学生与性别有关?
非体育健康A类学生 | 体育健康A类学生 | 合计 | |
男生 | |||
女生 | |||
合计 |
(Ⅱ)将每天自主参加体育锻炼时间不低于50分钟的学生称为体育健康![]() 类学生,已知体育健康
类学生,已知体育健康![]() 类学生中有2名女生,若从体育健康
类学生中有2名女生,若从体育健康![]() 类学生中任意选取2人,求至少有1名女生的概率.
类学生中任意选取2人,求至少有1名女生的概率.
附:
P( | 0.05 | 0.010 | 0.005 |
| 3.841 | 6.635 | 7.879 |
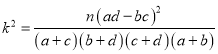
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O:x2+y2=3上的一动点M在x轴上的投影为N,点P满足![]() .
.
(1)求动点P的轨迹C的方程;
(2)若直线l与圆O相切,且交曲线C于点A,B,试求|AB|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某景区内有一半圆形花圃,其直径AB为6,O是圆心,且OC⊥AB.在OC上有一座观赏亭Q,其中∠AQC=![]() ,.计划在
,.计划在![]() 上再建一座观赏亭P,记∠POB=θ
上再建一座观赏亭P,记∠POB=θ![]() .
.
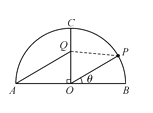
(1)当θ=![]() 时,求∠OPQ的大小;
时,求∠OPQ的大小;
(2)当∠OPQ越大时,游客在观赏亭P处的观赏效果越佳,求游客在观赏亭P处的观赏效果最佳时,角θ的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别为△ABC三个内角A,B,C的对边,且acos C+![]() asin C-b-c=0.
asin C-b-c=0.
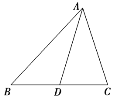
(1)求A;
(2)若AD为BC边上的中线,cos B=![]() ,AD=
,AD=![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com