练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知F1、F2是某等轴双曲线的两个焦点，P为该双曲线上一点，若PF1⊥PF2 ， 则以F1、F2为焦点且经过点P的椭圆的离心率是．

    【答案】
    【解析】解：由题意可设双曲线方程为x2﹣y2=1，

    ∴a2=b2=1，c2=a2+b2=2，

    可得|F1F2|=2 ，

    ∵PF1⊥PF2，

    ∴|PF1|2+|PF2|2=|F1F2|2=8，

    又∵P为双曲线x2﹣y2=1上一点，

    ∴||PF1|﹣|PF2||=2a=2，

    ∴（|PF1|﹣|PF2|）2=4，

    因此（|PF1|+|PF2|）2=2（|PF1|2+|PF2|2）﹣（|PF1|﹣|PF2|）2=12

    ∴|PF1|+|PF2|的值为2 ，

    ∴以F1，F2为焦点且经过P的椭圆的离心率为 = ．

    所以答案是： ．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】若不等式[2tx2﹣（t2﹣1）x+2]lnx≤0对任意x∈（0，+∞）恒成立，则实数t的值是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】f（x）=Acos（ωx+φ）（A，ω＞0）的图象如图所示，为得到g（x）=﹣Asin（ωx+ ）的图象，可以将f（x）的图象（ ）
    A.向右平移 个单位长度
    B.向右平移 个单位长度
    C.向左平移 个单位长度
    D.向左平移 个单位长度

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义在 上的奇函数 满足： ，且在区间 上单调递减，则不等式 的解集是（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列说法正确的是（ ）
    A.“p∨q”是“p∧q”的充分不必要条件
    B.样本10，6，8，5，6的标准差是3.3
    C.K2是用来判断两个分类变量是否相关的随机变量，当K2的值很小时可以推定两类变量不相关
    D.设有一个回归直线方程为 =2﹣1.5x，则变量x每增加一个单位， 平均减少1.5个单位．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 ，
    （1）若 ，求 在区间 上的最小值；
    （2）若 在区间 上有最大值 ，求实数 的值

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，有一边长为6的正方形铁片，在铁片的四角各截去一个边长为x的小正方形后，沿图中虚线部分折起，做成一个无盖方盒．
    （1）试用x表示方盒的容积V（x），并写出x的范围；
    （2）求方盒容积V（x）的最大值及相应x的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线l在x轴上的截距比在y轴上的截距大1，且过点(6，-2)，求直线l的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】长方体ABCD－A1B1C1D1中，AB＝BC＝2，D1D＝3，点M是B1C1的中点，点N是AB的中点．建立如图所示的空间直角坐标系.

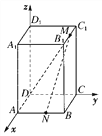
    (1)写出点D、N、M的坐标；

    (2)求线段MD、MN的长度．

    查看答案和解析>>

    同步练习册答案