
已知 次多项式
次多项式 .秦九韶给出的一种算法中,计算
.秦九韶给出的一种算法中,计算 的值需要
的值需要 次算法,计算
次算法,计算 的值共需要9次运算(6次乘法,3次加法),那么计算
的值共需要9次运算(6次乘法,3次加法),那么计算 的值共需要 次运算.
的值共需要 次运算.
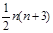
【解析】
试题分析:解:在利用常规算法计算多项式Pn(x)=a0xn+a1xn-1+…+an-1x+an的值时,算a0xn项需要n乘法,则在计算时共需要乘法:n+(n-1)+(n-2)+…+2+1=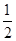 n(n+1)
n(n+1)
次需要加法:n次,则计算Pn(x0)的值共需要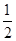 n(n+3)次运算.,在使用秦九韶算法计算多项式Pn(x)=a0xn+a1xn-1+…+an-1x+an的值时,共需要乘法:n次,需要加法:n次,则计算Pn(x0)的值共需要2n算.故答案为:
n(n+3)次运算.,在使用秦九韶算法计算多项式Pn(x)=a0xn+a1xn-1+…+an-1x+an的值时,共需要乘法:n次,需要加法:n次,则计算Pn(x0)的值共需要2n算.故答案为: 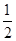 n(n+3),
n(n+3),
考点:算法的概念
点评:这是一道新运算类的题目,其特点一般是“新”而不“难”,处理的方法一般为:根据新运算的定义,将已知中的数据代入进行运算,易得最终结果


科目:高中数学 来源: 题型:
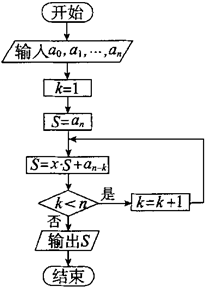 已知n次多项式Sn(x)=
已知n次多项式Sn(x)=| n |
 |
| i=0 |
| n(n+3) |
| 2 |
| n(n+3) |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com