
设 :
: ,
,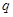 :关于
:关于 的不等式
的不等式 的解集是空集,试确定实数
的解集是空集,试确定实数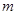 的取值范围,使得
的取值范围,使得 或
或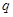 为真命题,
为真命题, 且
且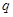 为假命题。
为假命题。
(-∞,-2)∪[0,2]∪[3,+∞).
解析试题分析:解不等式 得0≤m<3,∵不等式x2-4x+m2≤0的解集为∅,∴Δ=16-4m2<0,∴m<-2或m>2. 因为
得0≤m<3,∵不等式x2-4x+m2≤0的解集为∅,∴Δ=16-4m2<0,∴m<-2或m>2. 因为 或
或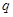 为真命题,
为真命题, 且
且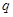 为假命题,所以p与q有且仅有一真.当p成立而q不成立时,0≤m≤2. 当p不成立而q成立时,m<-2或m≥3. 综上所述,m∈(-∞,-2)∪[0,2]∪[3,+∞).
为假命题,所以p与q有且仅有一真.当p成立而q不成立时,0≤m≤2. 当p不成立而q成立时,m<-2或m≥3. 综上所述,m∈(-∞,-2)∪[0,2]∪[3,+∞).
解: 化为
化为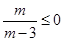 ,∴0≤m<3. ------4分
,∴0≤m<3. ------4分
∵不等式x2-4x+m2≤0的解集为∅,∴Δ=16-4m2<0,∴m<-2或m>2. ------8分
∵p或q真,p且q假,∴p与q有且仅有一真.------9分
当p成立而q不成立时,0≤m≤2. ------11分
当p不成立而q成立时,m<-2或m≥3. ------13分
综上所述,m∈(-∞,-2)∪[0,2]∪[3,+∞).------14分
考点:复合命题真假


科目:高中数学 来源: 题型:解答题
分别写出下列命题的逆命题、逆否命题,并判断它们的真假:
(1)若q<1,则方程x2+2x+q=0有实根;
(2)若x2+y2=0,则x,y全为零.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设命题p:函数f(x)=lg(ax2-4x+a)的定义域为R;命题q:不等式2x2+x>2+ax,在x∈(-∞,-1)上恒成立,如果命题“p∨q”为真命题,命题“p∧q”为假命题,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com