解:(1)∵函数f(x)为定义在R上的奇函数,
∴当x=0时,f(0)=0;
设x<0,则-x>0,且满足表达式f(x)=lg(x+1)+x
2,
∴f(-x)=lg(-x+1)+(-x)
2=lg(-x+1)+x
2,
又∵函数f(x)为定义在R上的奇函数,
∴f(-x)=-f(x),
∴-f(x)=lg(-x+1)+x
2,
即f(x)=-lg(-x+1)-x
2,
故当x为实数时f(x)的表达式为f(x)=
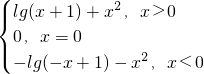
.
(2)将-x代入
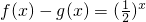
①,得f(-x)-g(-x)=(

)
-x=2
x,
∵f(x)为偶函数,g(x)为奇函数,
∴f(-x)=f(x),g(-x)=-g(x),
∴f(x)+g(x)=2
x,②
①②联立,解得f(x)=

,g(x)=
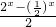
,
∴f(1)=

,g(0)=0,g(-2)=
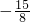
,
故f(1)>g(0)>g(-2).
分析:(1)由已知条件,要求x为实数时f(x) 的表达式,只须求出x≤0时的表达式,由奇函数的性质易得当x=0时,f(0)=0,f(-x)=-f(x),逐步转化即可求解.
(2)根据奇偶性的定义,将-x代入已知解析式,整理可得f(x)与g(x)的又一关系式,两者联立,解方程组,即可求得f(x)与g(x)的解析式,故f(1),g(0),g(-2)的值可求,进而比较其大小.
点评:(1)利用函数的奇偶性求函数某一部分的表达式的步骤:(1)在哪个区间求解析式,x就设在那个区间里;(2)利用已知区间的解析式进行代入;(3)利用f(x)的奇偶性把f(-x)写成-f(x)或f(x),从而解出f(x).
(2)解决本题的关键是灵活应用函数奇偶性的定义,将-x代入原式进行化简,运用了转化思想和方程思想,考查了学生运算能力和逻辑推理能力.

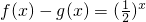 ,试比较f(1),g(0),g(-2)的大小.
,试比较f(1),g(0),g(-2)的大小.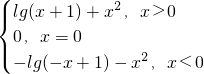 .
.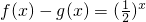 ①,得f(-x)-g(-x)=(
①,得f(-x)-g(-x)=( )-x=2x,
)-x=2x, ,g(x)=
,g(x)=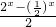 ,
, ,g(0)=0,g(-2)=
,g(0)=0,g(-2)=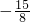 ,
,
