
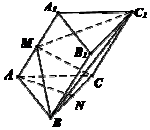
 如图,在三棱锥ABC-A1B1C1中,AC=BC=AA1=2,∠ACB=90°,∠A1AC=60°,M,N分别是线段AA1,BC上的点,且NC=NB,AA1⊥平面BCM.
如图,在三棱锥ABC-A1B1C1中,AC=BC=AA1=2,∠ACB=90°,∠A1AC=60°,M,N分别是线段AA1,BC上的点,且NC=NB,AA1⊥平面BCM.分析 (1)设O 为AC 中点,D 为AB 中点,以O 为坐标原点,OD,OC,OA1 为x,y,z 轴建立空间直角坐标系,求出相关点的坐标,求出平面BC1M 的法向量,平面BCM的法向量,然后证明AN∥平面BC1M.
(2)求出面BB1C1 的法向量,平面BC1M 的法向量,设二面角C1-BM-C 的平面角的大小为$θ(\frac{π}{2}<θ<π)$,利用向量的数量积求解二面角M-BC1-B1的余弦值.
另解:(1)取BC1的中点H,连接NH.(1)证明NH∥AM,MH∥AN.然后证明AN∥平面BC1M.
(2)说明∠MHC为二面角M-BC1-C的平面角.通过求解三角形结合二面角M-BC1-C的平面角的补角为∠MHC,求解二面角M-BC1-C的余弦值,
解答 解:设O 为AC 中点,D 为AB 中点,以O 为坐标原点,OD,OC,OA1 为x,y,z 轴建立空间直角坐标系,则$A(0,-1,0),B(2,1,0),C(0,1,0),{A_1}(0,0,\sqrt{3}),{B_1}(2,2,\sqrt{3}),{C_1}(0,2,\sqrt{3}),N(1,1,0)$ 设$\overrightarrow{AM}=t\overrightarrow{A{A_1}}(0≤t≤1)$,即$({x_M},{y_M}+1,{z_M})=t(0,1,\sqrt{3})$,从而$M(0,t-1,\sqrt{3}t)$ 显然$\overrightarrow{A{A_1}}=(0,1,\sqrt{3})$,$\overrightarrow{BM}=(-2,t-2,\sqrt{3}t)$,$\overrightarrow{BC}=(-2,0,0)$,则要使$\overrightarrow{A{A}_{1}}⊥$平面BCM,则$\overrightarrow{A{A_1}}•\overrightarrow{BM}=0$ 且$\overrightarrow{A{A_1}}•\overrightarrow{BC}=0$,即$t-2+\sqrt{3}•\sqrt{3}t=0$,故$t=\frac{1}{2}$,从而点M 的坐标为$M(0,-\frac{1}{2},\frac{{\sqrt{3}}}{2})$,即M 为AA1 中点.(1)设平面BC1M 的法向量$\overrightarrow{n_1}=({x_1},{y_1},{z_1})$,由于$\overrightarrow{BM}=(-2,-\frac{3}{2},\frac{{\sqrt{3}}}{2})$,$\overrightarrow{B{C_1}}=(-2,1,\sqrt{3})$,由于$\left\{\begin{array}{l}\overrightarrow{BM}•\overrightarrow{n_1}=0\\ \overrightarrow{B{C_1}}•\overrightarrow{n_1}=0\end{array}\right.$,则$\left\{\begin{array}{l}-2x-\frac{3}{2}y+\frac{{\sqrt{3}}}{2}z=0\\-2x+y+\sqrt{3}z=0\end{array}\right.$,从而$x:y:z=2\sqrt{3}:(-\sqrt{3}):5$,取$\overrightarrow{n_1}=(2\sqrt{3},-\sqrt{3},5)$ 由于$\overrightarrow{AN}=(1,2,0)$,从而$\overrightarrow{AN}•\overrightarrow{n_1}=1×2\sqrt{2}-2×\sqrt{3}=0$,从而$\overrightarrow{AN}⊥\overrightarrow{n_1}$,又$\overrightarrow{AN}∥$平面BC1M,从而AN∥平面BC1M (2)设平面BB1C1 的法向量$\overrightarrow{n_2}=({x_2},{y_2},{z_2})$,由于$\overrightarrow{B{B_1}}=(0,1,\sqrt{3})$,$\overrightarrow{B{C_1}}=(-2,1,\sqrt{3})$ 由于$\left\{\begin{array}{l}\overrightarrow{B{B_1}}•\overrightarrow{n_2}=0\\ \overrightarrow{B{C_1}}•\overrightarrow{n_1}=0\end{array}\right.$,则$\left\{\begin{array}{l}{y_2}+\sqrt{3}{z_2}=0\\-2{x_1}+{y_2}+\sqrt{3}{z_2}=0\end{array}\right.$,从而$x:y:z=0:(-\sqrt{3}):1$,取$\overrightarrow{n_2}=(0,-\sqrt{3},1)$ 又平面BC1M 的法向量$\overrightarrow{n_1}=(2\sqrt{3},-\sqrt{3},5)$ 设二面角C1-BM-C 的平面角的大小为$θ(\frac{π}{2}<θ<π)$则$cosθ=-|cos<\overrightarrow{n_1},\overrightarrow{n_2}>|=|\frac{{\overrightarrow{n_1}•\overrightarrow{n_2}}}{{|\overrightarrow{n_1}||\overrightarrow{n_2}|}}|=-\frac{8}{{2×\sqrt{40}}}=-\frac{{\sqrt{10}}}{5}$综上所述,二面角M-BC1-B1的余弦值为$-\frac{{\sqrt{10}}}{5}$.
另解:(1)取BC1的中点H,连接NH.(1)由于AA1⊥平面BCM,则AA1⊥CM,考虑到△AA1C为正三角形,从而M为AA1中点.由于H,N为BC1,BC中点,从而$NH∥\frac{1}{2}C{C_1}$.又$AM\underline{\underline{∥}}\frac{1}{2}C{C_1}$,从而NH∥AM,故AMHN为平行四边形,从而MH∥AN.又MH?平面BC1M,AN?平面BC1M,从而AN∥平面BC1M.
(2)由于侧面ACC1A1⊥底面ABC,平面ACC1A1∩底面ABC=AC,BC⊥AC,BC?平面ABC,从而BC⊥平面ACC1A1,又MC?平面ACC1A1,从而MC⊥BC.又MC⊥CC1,从而BC∩CC1=C,从而MC⊥平面BCC1B1.又BC=CC1,H为BC1的中点,从而CH⊥BC1,故∠MHC为二面角M-BC1-C的平面角.又$MC=\sqrt{3}$,$CH=\sqrt{2}$,$MH=\sqrt{5}$,从而$cos∠MHC=\frac{CH}{MH}=\frac{{\sqrt{2}}}{{\sqrt{5}}}=\frac{{\sqrt{10}}}{5}$.又二面角M-BC1-C的平面角的补角为∠MHC,二面角M-BC1-C的余弦值为$-\frac{{\sqrt{10}}}{5}$.
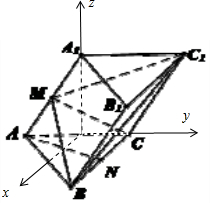
点评 本题考查直线与平面平行的判定定理的应用,二面角的平面角的求法,考查空间想象能力以及计算能力.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{13}$ | B. | $\frac{5}{7}$ | C. | $\frac{17}{25}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
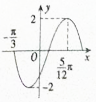 函数f(x)=2sin(ωx+φ$)(ω>0,-\frac{π}{2}<$(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则f(x)的图象可由函数g(x)=2sinωx的图象至少向右平移$\frac{π}{6}$个单位得到.
函数f(x)=2sin(ωx+φ$)(ω>0,-\frac{π}{2}<$(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则f(x)的图象可由函数g(x)=2sinωx的图象至少向右平移$\frac{π}{6}$个单位得到.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-∞,1] | C. | (-∞,-4)∪(-4,1] | D. | (-∞,-4)∪(-4,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2.5% | B. | 95% | C. | 97.5% | D. | 不具有相关性 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<$\frac{1}{2}$} | B. | {x|x<0或0<x<$\frac{1}{2}$} | C. | {x|x>$\frac{1}{2}$} | D. | {x|0<x<$\frac{1}{2}$} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 参加书法班 | 未参加书法班 | |
| 参加演讲班 | 8 | 5 |
| 未参加演讲班 | 2 | 33 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com