
【题目】如图,四棱锥![]() 的底面是正方形,
的底面是正方形, ![]() ,点E在棱PB上.
,点E在棱PB上.
(Ⅰ)求证:平面![]() ;
;
(Ⅱ)当![]() 且E为PB的中点时,求AE与平面PDB所成的角的大小.
且E为PB的中点时,求AE与平面PDB所成的角的大小.

【答案】(1)见解析 (2) ![]()
【解析】试题分析:(Ⅰ)欲证平面AEC⊥平面PDB,根据面面垂直的判定定理可知在平面AEC内一直线与平面PDB垂直,而根据题意可得AC⊥平面PDB;(Ⅱ)设AC∩BD=O,连接OE,根据线面所成角的定义可知∠AEO为AE与平面PDB所的角,在Rt△AOE中求出此角即可
试题解析:(1)证明:∵四边形ABCD是正方形,∴AC⊥BD,∵![]() ,
,
∴PD⊥AC,∴AC⊥平面PDB,
∴平面![]() .
.
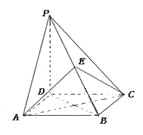
(2)解:设AC∩BD=O,连接OE,
由(Ⅰ)知AC⊥平面PDB于O,
∴∠AEO为AE与平面PDB所的角,
∵ O,E分别为DB、PB的中点,
∴OE//PD, ![]() ,
,
在Rt△AOE中, ![]() ,∴
,∴![]() ,
,
即AE与平面PDB所成的角的大小为![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在极坐标系中,圆![]() 的极坐标方程为
的极坐标方程为![]() ,若以极点
,若以极点![]() 为原点,极轴所在的直线为
为原点,极轴所在的直线为![]() 轴建立平面直角坐标系.
轴建立平面直角坐标系.
(1)求圆![]() 的参数方程;
的参数方程;
(2)在直线坐标系中,点![]() 是圆
是圆![]() 上的动点,试求
上的动点,试求![]() 的最大值,并求出此时点
的最大值,并求出此时点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=ax2+(a﹣2)x﹣2(a∈R).
(1)解关于x的不等式f(x)≥0;
(2)若a>0,当﹣1≤x≤1时,f(x)≤0时恒成立,求a的取值范围.
(3)若当﹣1<a<1时,f(x)>0时恒成立,求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cosx(sinx﹣cosx)+1,x∈R.
(1)求函数f(x)的最小正周期;
(2)求函数f(x)在区间 ![]() 上的最小值和最大值.
上的最小值和最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数f(x)=4sin(2x ![]() )(x∈R),有下列命题: ①y=f(x)的表达式可改写为y=4cos(2x﹣
)(x∈R),有下列命题: ①y=f(x)的表达式可改写为y=4cos(2x﹣ ![]() );
);
②y=f(x)是以2π为最小正周期的周期函数;
③y=f(x)的图象关于点 ![]() 对称;
对称;
④y=f(x)的图象关于直线x=﹣ ![]() 对称.
对称.
其中正确的命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】求椭圆的标准方程
(1)已知某椭圆的左右焦点分别为F1(﹣1,0),F2(1,0),且经过点P( ![]() ,
, ![]() ),求该椭圆的标准方程;
),求该椭圆的标准方程;
(2)已知某椭圆过点( ![]() ,﹣1),(﹣1,
,﹣1),(﹣1, ![]() ),求该椭圆的标准方程.
),求该椭圆的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC满足| ![]() |=3,|
|=3,| ![]() |=4,O是△ABC所在平面内一点,满足|
|=4,O是△ABC所在平面内一点,满足| ![]() |=|
|=| ![]() |=|
|=| ![]() |,且
|,且 ![]() =λ
=λ ![]() +
+ ![]()
![]() (λ∈R),则cos∠BAC= .
(λ∈R),则cos∠BAC= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com