
ЁОЬтФПЁПдкЁАаТСуЪлЁБФЃЪНЕФБГОАЯТЃЌФГДѓаЭСуЪлЙЋЫОпфЭЦЙуЯпЯТЗжЕъЃЌМЦЛЎдк![]() ЪаЕФ
ЪаЕФ![]() ЧјПЊЩшЗжЕъЃЌЮЊСЫШЗЖЈдкИУЧјПЊЩшЗжЕъЕФИіЪ§ЃЌИУЙЋЫОЖдИУЪавбПЊЩшЗжЕъЬ§ЦфЫћЧјЕФЪ§ОнзїСЫГѕВНДІРэКѓЕУЕНЯТСаБэИёЃЎМЧ
ЧјПЊЩшЗжЕъЃЌЮЊСЫШЗЖЈдкИУЧјПЊЩшЗжЕъЕФИіЪ§ЃЌИУЙЋЫОЖдИУЪавбПЊЩшЗжЕъЬ§ЦфЫћЧјЕФЪ§ОнзїСЫГѕВНДІРэКѓЕУЕНЯТСаБэИёЃЎМЧ![]() БэЪОдкИїЧјПЊЩшЗжЕъЕФИіЪ§ЃЌ
БэЪОдкИїЧјПЊЩшЗжЕъЕФИіЪ§ЃЌ ![]() БэЪОетИі
БэЪОетИі![]() ИіЗжЕъЕФФъЪеШыжЎКЭЃЎ
ИіЗжЕъЕФФъЪеШыжЎКЭЃЎ
| 2 | 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 | 6 |
ЃЈ1ЃЉИУЙЋЫОвбОЙ§ГѕВНХаЖЯЃЌПЩгУЯпадЛиЙщФЃаЭФтКЯ![]() гы
гы![]() ЕФЙиЯЕЃЌЧѓ
ЕФЙиЯЕЃЌЧѓ![]() Йигк
Йигк![]() ЕФЯпадЛиЙщЗНГЬ
ЕФЯпадЛиЙщЗНГЬ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉМйЩшИУЙЋЫОдк![]() ЧјЛёЕУЕФзмФъРћШѓ
ЧјЛёЕУЕФзмФъРћШѓ![]() ЃЈЕЅЮЛЃКАйЭђдЊЃЉгы
ЃЈЕЅЮЛЃКАйЭђдЊЃЉгы![]() жЎМфЕФЙиЯЕЮЊ
жЎМфЕФЙиЯЕЮЊ![]() ЃЌЧыНсКЯЃЈ1ЃЉжаЕФЯпадЛиЙщЗНГЬЃЌЙРЫуИУЙЋЫОгІдк
ЃЌЧыНсКЯЃЈ1ЃЉжаЕФЯпадЛиЙщЗНГЬЃЌЙРЫуИУЙЋЫОгІдк![]() ЧјПЊЩшЖрЩйИіЗжЕъЪБЃЌВХФмЪЙ
ЧјПЊЩшЖрЩйИіЗжЕъЪБЃЌВХФмЪЙ![]() ЧјЦНОљУПИіЕъЕФФъРћШѓзюДѓЃП
ЧјЦНОљУПИіЕъЕФФъРћШѓзюДѓЃП
ЃЈВЮПМЙЋЪНЃК ![]() ЃЌЦфжа
ЃЌЦфжа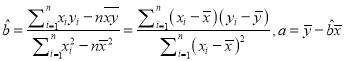 ЃЉ
ЃЉ
ЁОД№АИЁП(1) ![]() ;(2) ИУЙЋЫОгІПЊЩш4ИіЗжЕъЪБЃЌдкИУЧјЕФУПИіЗжЕъЕФЦНОљРћШѓзюДѓ.
;(2) ИУЙЋЫОгІПЊЩш4ИіЗжЕъЪБЃЌдкИУЧјЕФУПИіЗжЕъЕФЦНОљРћШѓзюДѓ.
ЁОНтЮіЁПЪдЬтЗжЮіЃК
ЃЈ1ЃЉИљОнЫљИјЪ§ОнЃЌАДееЙЋЪНМЦЫуЛиЙщЗНГЬжаЕФЯЕЪ§МДПЩЃЛ
ЃЈ2ЃЉРћгУЃЈ1ЃЉЕУРћШѓ![]() гыЗжЕъЪ§
гыЗжЕъЪ§![]() жЎМфЕФЙРМЦжЕЃЌМЦЫу
жЎМфЕФЙРМЦжЕЃЌМЦЫу![]() ЃЌгЩЛљБОВЛЕШЪНПЩЕУзюДѓжЕЃЎ
ЃЌгЩЛљБОВЛЕШЪНПЩЕУзюДѓжЕЃЎ
ЪдЬтНтЮіЃК
ЃЈ1ЃЉгЩБэжаЪ§ОнКЭВЮПМЪ§ОнЕУЃК ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ
Ёр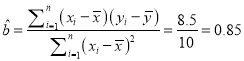 ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ
Ёр![]() ЃЎ
ЃЎ
ЃЈ2ЃЉгЩЬтвтЃЌПЩжЊзмЪеШыЕФдЄБЈжЕ![]() гы
гы![]() жЎМфЕФЙиЯЕЮЊЃК
жЎМфЕФЙиЯЕЮЊЃК ![]() ЃЌ
ЃЌ
ЩшИУЧјУПИіЗжЕъЕФЦНОљРћШѓЮЊ![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
ЙЪ![]() ЕФдЄБЈжЕ
ЕФдЄБЈжЕ![]() гы
гы![]() жЎМфЕФЙиЯЕЮЊ
жЎМфЕФЙиЯЕЮЊ![]() ЃЌ
ЃЌ
дђЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() ШЁЕНзюДѓжЕЃЌ
ШЁЕНзюДѓжЕЃЌ
ЙЪИУЙЋЫОгІПЊЩш4ИіЗжЕъЪБЃЌдкИУЧјЕФУПИіЗжЕъЕФЦНОљРћШѓзюДѓЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшЖЈвхдкЃЈ0ЃЌ+ЁоЃЉЩЯЕФКЏЪ§fЃЈxЃЉТњзуxfЁфЃЈxЃЉЉfЃЈxЃЉ=xlnxЃЌfЃЈ ![]() ЃЉ=
ЃЉ= ![]() ЃЌдђfЃЈxЃЉЃЈ ЃЉ
ЃЌдђfЃЈxЃЉЃЈ ЃЉ
A.гаМЋДѓжЕЃЌЮоМЋаЁжЕ
B.гаМЋаЁжЕЃЌЮоМЋДѓжЕ
C.МШгаМЋДѓжЕЃЌгжгаМЋаЁжЕ
D.МШЮоМЋДѓжЕЃЌвВЮоМЋаЁжЕ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§Са{an}Тњзуa1=1ЃЌan+1=3an+1ЃЎ
ЃЈ1ЃЉжЄУї{an+ ![]() }ЪЧЕШБШЪ§СаЃЌВЂЧѓ{an}ЕФЭЈЯюЙЋЪНЃЛ
}ЪЧЕШБШЪ§СаЃЌВЂЧѓ{an}ЕФЭЈЯюЙЋЪНЃЛ
ЃЈ2ЃЉжЄУїЃК ![]() +
+ ![]() +Ё+
+Ё+ ![]() ЃМ
ЃМ ![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ=AsinЃЈx+ ![]() ЃЉЃЌxЁЪRЃЌЧвfЃЈ
ЃЉЃЌxЁЪRЃЌЧвfЃЈ ![]() ЃЉ=
ЃЉ= ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓAЕФжЕЃЛ
ЃЈ2ЃЉШєfЃЈІШЃЉ+fЃЈЉІШЃЉ= ![]() ЃЌІШЁЪЃЈ0ЃЌ
ЃЌІШЁЪЃЈ0ЃЌ ![]() ЃЉЃЌЧѓfЃЈ
ЃЉЃЌЧѓfЃЈ ![]() ЉІШЃЉЃЎ
ЉІШЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ=x3Љtx2+3xЃЌШєЖдгкШЮвтЕФaЁЪ[1ЃЌ2]ЃЌbЁЪЃЈ2ЃЌ3]ЃЌКЏЪ§fЃЈxЃЉдкЧјМфЃЈaЃЌbЃЉЩЯЕЅЕїЕнМѕЃЌдђЪЕЪ§tЕФШЁжЕЗЖЮЇЪЧЃЈЁЁЁЁЃЉ
A.ЃЈЉЁоЃЌ3]
B.ЃЈЉЁоЃЌ5]
C.[3ЃЌ+ЁоЃЉ
D.[5ЃЌ+ЁоЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкРтГЄЮЊ1ЕФе§ЗНЬх![]() жаЃЌЕуEЁЂFЗжБ№ЪЧРтBCЃЌ
жаЃЌЕуEЁЂFЗжБ№ЪЧРтBCЃЌ![]() ЕФжаЕуЃЌPЪЧВрУц
ЕФжаЕуЃЌPЪЧВрУц![]() ФквЛЕуЃЌШє
ФквЛЕуЃЌШє![]() ЁЮЦНУцAEFЃЌдђЯпЖЮ
ЁЮЦНУцAEFЃЌдђЯпЖЮ![]() ГЄЖШЕФШЁжЕЗЖЮЇЪЧ_________ЁЃ
ГЄЖШЕФШЁжЕЗЖЮЇЪЧ_________ЁЃ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЕуPЪЧЦНааЫФБпаЮABCDЫљдкЦНУцЭтвЛЕуЃЌMЁЂNЗжБ№ЪЧABЁЂPCЕФжаЕуЃЎ
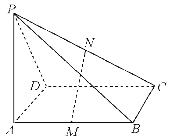
ЃЈ1ЃЉЧѓжЄЃКMNЁЮЦНУцPADЃЛ
ЃЈ2ЃЉдкPBЩЯШЗЖЈвЛИіЕуQЃЌЪЙЦНУцMNQЁЮЦНУцPAD.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊжБЯпlЙ§жБЯпxЉyЉ1=0гыжБЯп2x+yЉ5=0ЕФНЛЕуPЃЎ
ЃЈ1ЃЉШєlгыжБЯпx+3yЉ1=0ДЙжБЃЌЧѓlЕФЗНГЬЃЛ
ЃЈ2ЃЉЕуAЃЈЉ1ЃЌ3ЃЉКЭЕуBЃЈ3ЃЌ1ЃЉЕНжБЯпlЕФОрРыЯрЕШЃЌЧѓжБЯпlЕФЗНГЬЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§Са ![]() ЕФЭЈЯюЙЋЪНЪЧ
ЕФЭЈЯюЙЋЪНЪЧ ![]() ЃЌФЧУДетИіЪ§СаЪЧЃЈ ЃЉ
ЃЌФЧУДетИіЪ§СаЪЧЃЈ ЃЉ
A.ЕндіЪ§Са
B.ЕнМѕЪ§Са
C.ГЃЪ§Са
D.АкЖЏЪ§Са
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com