
分析 由已知中定义f1(x)=f′(x),f2(x)=[f1(x)]′,…,fn+1(x)=[fn(x)]′,n∈N*.
结合f1(x)=$\frac{1-x}{{e}^{x}}$,f2(x)=$\frac{x-2}{{e}^{x}}$,f3(x)=$\frac{3-x}{{e}^{x}}$,…,分析出fn(x)解析式随n变化的规律,可得答案
解答 解:∵f1(x)=$\frac{1-x}{{e}^{x}}$=$\frac{(-1)^{1}(x-1)}{{e}^{x}}$,f2(x)=$\frac{x-2}{{e}^{x}}$=$\frac{(-1)^{2}(x-2)}{{e}^{x}}$,f3(x)=$\frac{3-x}{{e}^{x}}$=$\frac{(-1)^{3}(x-3)}{{e}^{x}}$,…,
由此归纳可得:fn(x)=$\frac{{{{(-1)}^n}(x-n)}}{e^x}$,
故答案为:$\frac{{{{(-1)}^n}(x-n)}}{e^x}$
点评 本题考查了函数求导以及归纳推理;归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | an=2n-1 | B. | an=3n | C. | 2 | D. | an=5n |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-∞,-\frac{1}{2}})∪[{\frac{1}{2},1}]$ | B. | $[{\frac{1}{2},1}]$ | C. | (0,1] | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
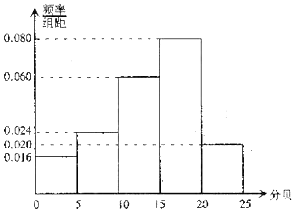 人耳的听力情况可以用电子测听器检测,正常人听力的等级为0-25db(分贝),并规定测试值在区间(0,5]为非常优秀,测试值在区间(5,10]为优秀,某班50名同学都进行了听力测试,所得测试值制成频率分布直方图:
人耳的听力情况可以用电子测听器检测,正常人听力的等级为0-25db(分贝),并规定测试值在区间(0,5]为非常优秀,测试值在区间(5,10]为优秀,某班50名同学都进行了听力测试,所得测试值制成频率分布直方图:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{{1+\sqrt{3}}}{2}$ | C. | $\frac{3}{2}$ | D. | $1+\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com