
【题目】已知函数![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,若
时,若![]() 对任意的
对任意的![]() 恒成立,求实数
恒成立,求实数![]() 的值;
的值;
(3)求证:![]() .
.
 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知圆![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).若直线
为参数).若直线![]() 与圆
与圆![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() .
.
(Ⅰ)写出圆![]() 的直角坐标方程,并求圆心的坐标与半径;
的直角坐标方程,并求圆心的坐标与半径;
(Ⅱ)若弦长![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的离心率
的离心率![]() ,圆
,圆![]() 与直线
与直线![]() 相切,
相切,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 任作一直线
任作一直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,记
两点,记![]() ,若在线段
,若在线段![]() 上取一点
上取一点![]() ,使得
,使得![]() ,试判断当直线
,试判断当直线![]() 运动时,点
运动时,点![]() 是否在某一定直一上运动?若是,请求出该定直线的方程;若不是,请说明理由.
是否在某一定直一上运动?若是,请求出该定直线的方程;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某制造厂商10月份生产了一批乒乓球,从中随机抽取![]() 个进行检查,测得每个球的直径(单位:
个进行检查,测得每个球的直径(单位:![]() ),将数据进行分组,得到如下频率分布表:
),将数据进行分组,得到如下频率分布表:

(1)求![]() 、
、![]() 、
、![]() 及
及![]() 、
、![]() 的值,并画出频率分布直方图(结果保留两位小数);
的值,并画出频率分布直方图(结果保留两位小数);
(2)已知标准乒乓球的直径为![]() ,直径误差不超过
,直径误差不超过![]() 的为五星乒乓球,若这批乒乓球共有
的为五星乒乓球,若这批乒乓球共有![]() 个,试估计其中五星乒乓球的数目;
个,试估计其中五星乒乓球的数目;
(3)统计方法中,同一组数据常用该组区间的中点值(例如区间![]() 的中点值是
的中点值是![]() )作为代表,估计这批乒乓球直径的平均值和中位数.
)作为代表,估计这批乒乓球直径的平均值和中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市经营一批产品,在市场销售中发现此产品在30天内的日销售量P(件)与日期![]() )之间满足
)之间满足![]() ,已知第5日的销售量为55件,第10日的销售量为50件。
,已知第5日的销售量为55件,第10日的销售量为50件。
(1)求第20日的销售量; (2)若销售单价Q(元/件)与![]() 的关系式为
的关系式为![]() ,求日销售额
,求日销售额![]() 的最大值。
的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校1800名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组![]() ,第二组
,第二组![]() ,第五组
,第五组![]() ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.
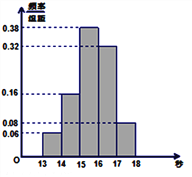
(1)若成绩小于15秒认为良好,求该样本在这次百米测试中成绩良好的人数;
(2)请估计学校1800名学生中,成绩属于第四组的人数;
(3)请根据频率分布直方图,求样本数据的众数、中位数、平均数和方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,公园有一块边长为![]() 的等边
的等边![]() 的边角地,现修成草坪,图中
的边角地,现修成草坪,图中![]() 把草坪分成面积相等的两部分,
把草坪分成面积相等的两部分,![]() 在
在![]() 上,
上,![]() 在
在![]() 上.
上.

(1)设![]() (
(![]() ),
),![]() ,求用
,求用![]() 表示
表示![]() 的函数关系式;
的函数关系式;
(2)如果![]() 是灌溉水管,为节约成本,希望它最短,
是灌溉水管,为节约成本,希望它最短,![]() 的位置应在哪里?如果
的位置应在哪里?如果![]() 是参观线路,则希望它最长,
是参观线路,则希望它最长,![]() 的位置又应在哪里?请说明理由.
的位置又应在哪里?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com