分析:(1)λ=1时,
=,以C为原点,CB为x轴,DC为y轴,CC
1为z轴,建立空间直角坐标系,则
=(0,2,2),
=(-1,0,2),设平面FDE的法向量为
,则
=(0,0,1),设平面FDE的法向量为
=(x,y,z),由
•=0,•=0,得
=(2,-1,1),由向量法能求出二面角F-DE-C的余弦值.
(2)由D
1(0,-2,4),B(2,0,0),E(1,0,0)设F(0,0,t),则
=(-2,-2,4),
=(-1,0,t),要使EF⊥BD
1,只要
•=0,由此能求出λ.
解答:解:(1)λ=1时,
=,
以C为原点,CB为x轴,DC为y轴,CC
1为z轴,建立空间直角坐标系,
∵正四棱柱ABCD-A
1B
1C
1D
1中,AB=2,AA
1=4,E为BC的中点,
∴E(1,0,0),F(0,0,2),D(0,-2,0),F(0,0,2),
∴
=(0,2,2),
=(-1,0,2),
设平面FDE的法向量为
,则
=(0,0,1),
设平面FDE的法向量为
=(x,y,z),则
•=0,•=0,
∴
,
∴
=(2,-1,1),
∴
cos<,>= =
,
∴二面角F-DE-C的余弦值为
.
(2)∵D
1(0,-2,4),B(2,0,0),E(1,0,0)
设F(0,0,t),则
=(-2,-2,4),
=(-1,0,t),
∵EF⊥BD
1,
∴
•=0,
∴2+4t=0,
解得t=-
.
∴F(0,0,-
)
∴
=(0,0,-),
=(0,0,),
∴λ=
=-9.
点评:本题考查二面角的余弦值的求法和求λ为何值时,有BD1⊥EF.解题时要认真审题,仔细解答,注意合理地把空间问题转化为平面问题,注意向量法的灵活运用.

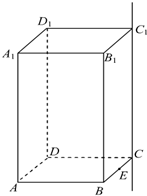 如图,已知正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=4,E为BC的中点,F为直线CC1上的动点,设
如图,已知正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=4,E为BC的中点,F为直线CC1上的动点,设

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案 如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.
如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a. 如图,已知正四棱柱ABCD-A1B1C1D1 的底面边长为3,侧棱长为4,连接A1B,过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E.
如图,已知正四棱柱ABCD-A1B1C1D1 的底面边长为3,侧棱长为4,连接A1B,过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E.
 如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.
如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.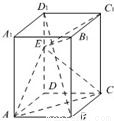 如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.
如图,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为45°,AB=a.