
|
解: 已知方程可化为: sin2(n+1)θ-sin2(n-1)θ = sin2nθ,[sin(n+1)θ+sin(n-1)θ][sin(n+1)θ-sin(n-1)θ]=sin2nθ 化简后, 得sin2nθ·sin2θ = sin2nθ ∵(n+1)θ、(n-1)θ、nθ是三角形的三个内角. ∴(n+1)θ+(n-1)θ+nθ = π, ∴3nθ = π, nθ = ∴sin2θ·sin sin2θ = sin ∴2θ = kπ+(-1)k 2θ = 当θ = ∴当θ = |
|
先把原方程转化为
sin2(n+1)θ-sin2(n-1)θ = sin2nθ,
再用平方差公式.
|


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:山西省四校2010届高三第一次联考文科数学试题 题型:044
已知点A(1,1),B(1,-1),C(![]() cos
cos![]() ,
,![]() sin
sin![]() )(
)(![]() ∈R),O为坐标原点.
∈R),O为坐标原点.
(Ⅰ)
若|(Ⅱ)若实数m,n满足m![]() +n
+n![]() =
=![]() ,求(m-3)2+n2的最大值.
,求(m-3)2+n2的最大值.
查看答案和解析>>
科目:高中数学 来源:2011年高三数学复习(第3章 三角函数与三角恒等变换):3.9 三角条件等式的证明(解析版) 题型:解答题
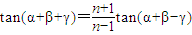 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com