【题目】设某大学的女生体重
（单位：
）与身高
（单位：
）具有线性相关关系。根据组样本数据
，用最小二乘法建立的回归方程为
，则下列结论中不正确的是( )
A.与具有正的线性相关关系
B.回归直线过样本点的中心
C.若该大学某女生身高增加
，则其体重约增加
D.若该大学某女生身高为
，则可断定其体重必为
全能测控一本好卷系列答案科目：高中数学 来源： 题型：
【题目】如图，A，B是半径为2的圆周上的定点，P为圆周上的动点，
是锐角，大小为β.图中阴影区域的面积的最大值为
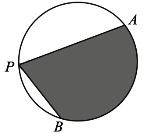
A. 4β+4cosβB. 4β+4sinβC. 2β+2cosβD. 2β+2sinβ
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】给出下列说法：
①命题“若
，则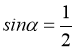
”的否命题是假命题；
②命题
，使
，则
；
③“
”是“函数
为偶函数”的充要条件；
④命题
“
，使
”，命题
“在
中，若
，则
”，那么命题
为真命题.
其中正确的个数是（ ）
A.1B.2C.3D.4
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
：
的两个焦点分别为
和
，短轴的两个端点分别为
和
，点
在椭圆上，且满足
，当
变化时，给出下列三个命题：
①点的轨迹关于
轴对称；②
的最小值为2；
③存在使得椭圆上满足条件的点仅有两个，
其中，所有正确命题的序号是__________．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某养殖场需要通过某装置对养殖车间进行恒温控制，为了解日用电量
与日平均气温
（℃）之间的关系，随机统计了某5天的用电量与当天平均气温，并制作了对照表：
日平均气温（℃） | 3 | 4 | 5 | 6 | 7 |
日用电量（ | 2.5 | 3 | 4 | 4.5 | 6 |
（Ⅰ）求
关于的线性回归方程；
（Ⅱ）请利用（Ⅰ）中的线性回归方程预测日平均气温为12℃时的日用电量.
附：回归直线的斜率和截距的最小二乘法估计公式分别为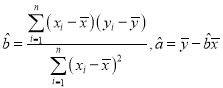
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，椭圆C：
的右准线方程为x＝4，右顶点为A，上顶点为B，右焦点为F，斜率为2的直线l经过点A，且点F到直线l的距离为
.
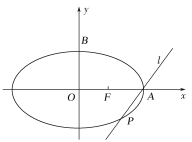
(1)求椭圆C的标准方程．
(2)将直线l绕点A旋转，它与椭圆C相交于另一点P，当B，F，P三点共线时，试确定直线l的斜率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知等比数列{an}的前n项和为Sn，且满足
(k∈R)．
（1）求k和数列{an}的通项公式；
（2）若数列{bn}满足bn＝
，求数列{bn}的前n项和Tn.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】定义域为R的偶函数
满足：对
,有
,且当
时,
若函数
在(0,+
)上至少有三个零点,则实数
的取值范围为
A. （0,
）B. （0,
）C. （0,
）D. （0,
）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
