
【题目】在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.
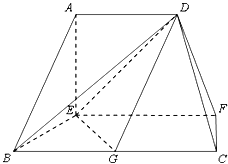
(Ⅰ)求证:AB∥平面DEG;
(Ⅱ)求证:BD⊥EG;
(Ⅲ)求多面体ADBEG的体积.
【答案】(Ⅰ)见解析(Ⅱ)见解析(Ⅲ)4
【解析】
(Ⅰ) 先证明四边形ADGB是平行四边形,可得AB∥DG,从而证明AB∥平面DEG.
(Ⅱ) 过D作DH∥AE交EF于H,则DH⊥平面BCFE,DH⊥EG,再证BH⊥EG,从而可证EG⊥平面BHD,故BD⊥EG.
(Ⅲ)要求多面体ADBEG的体积,利用分割的思想转化为VADBEG=VD﹣AEB+VD﹣BEG转化为求两个三棱锥的体积即可.
(Ⅰ)∵AD∥EF,EF∥BC,∴AD∥BC.
又∵BC=2AD,G是BC的中点,∴![]() ,∴四边形ADGB是平行四边形,∴AB∥DG,∵AB
,∴四边形ADGB是平行四边形,∴AB∥DG,∵AB![]() 平面DEG,DG
平面DEG,DG![]() 平面DEG,∴AB∥平面DEG.
平面DEG,∴AB∥平面DEG.
(Ⅱ)∵EF⊥平面AEB,AE平面AEB,∴EF⊥AE,
又AE⊥EB,EB∩EF=E,EB,EF平面BCFE,∴AE⊥平面BCFE.
过D作DH∥AE交EF于H,连接![]() ,则DH⊥平面BCFE.
,则DH⊥平面BCFE.
∵EG平面BCFE,∴DH⊥EG.
∵AD∥EH,DH∥AE,∴四边形AEHD平行四边形,∴EH=AD=2,
∴EH=BG=2,又EH∥BG,EH⊥BE,
∴四边形BGHE为正方形,∴BH⊥EG,
又BH∩DH=H,BH平面BHD,DH平面BHD,∴EG⊥平面BHD.
∵BD平面BHD,∴BD⊥EG.
(Ⅲ)∵EF⊥平面AEB,AD∥EF,∴AD⊥平面AEB,
由(2)知四边形BGHE为正方形,∴BE⊥BC.
∴VADBEG=VD﹣AEB+VD﹣BEG![]() 4.
4.



 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:高中数学 来源: 题型:
【题目】某大型公司为了切实保障员工的健康安全,贯彻好卫生防疫工作的相关要求,决定在全公司范围内举行一次乙肝普查.为此需要抽验669人的血样进行化验,由于人数较多,检疫部门制定了下列两种可供选择的方案.
方案一:将每个人的血分别化验,这时需要验669次.
方案二:按![]() 个人一组进行随机分组,把从每组
个人一组进行随机分组,把从每组![]() 个人抽来的血混合在一起进行检验,如果每个人的血均为阴性,则验出的结果呈阴性,这
个人抽来的血混合在一起进行检验,如果每个人的血均为阴性,则验出的结果呈阴性,这![]() 个人的血就只需检验一次(这时认为每个人的血化验
个人的血就只需检验一次(这时认为每个人的血化验![]() 次);否则,若呈阳性,则需对这
次);否则,若呈阳性,则需对这![]() 个人的血样再分别进行一次化验,这时该组
个人的血样再分别进行一次化验,这时该组![]() 个人的血总共需要化验
个人的血总共需要化验![]() 次.
次.
假设此次普查中每个人的血样化验呈阳性的概率为![]() ,且这些人之间的试验反应相互独立.
,且这些人之间的试验反应相互独立.
(1)设方案二中,某组![]() 个人中每个人的血化验次数为
个人中每个人的血化验次数为![]() ,求
,求![]() 的分布列.
的分布列.
(2)设![]() ,试比较方案二中,
,试比较方案二中,![]() 分别取2,3,4时,各需化验的平均总次数;并指出在这三种分组情况下,相比方案一,化验次数最多可以平均减少多少次?(最后结果四舍五入保留整数)
分别取2,3,4时,各需化验的平均总次数;并指出在这三种分组情况下,相比方案一,化验次数最多可以平均减少多少次?(最后结果四舍五入保留整数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,且椭圆过点
,且椭圆过点![]()
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 在椭圆
在椭圆![]() 上,
上,![]() 是坐标原点,若
是坐标原点,若![]() ,判定四边形
,判定四边形![]() 的面积是否为定值?若为定值,求出该定值;如果不是,请说明理由.
的面积是否为定值?若为定值,求出该定值;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于数列![]() ,若存在
,若存在![]() ,使得
,使得![]() 对任意
对任意![]() 都成立,则称数列
都成立,则称数列![]() 为“
为“![]() 折叠数列”.
折叠数列”.
(1)若![]() ,
,![]() ,判断数列
,判断数列![]() ,
,![]() 是否是“
是否是“![]() 折叠数列”,如果是,指出m的值;如果不是,请说明理由;
折叠数列”,如果是,指出m的值;如果不是,请说明理由;
(2)若![]() ,求所有的实数q,使得数列
,求所有的实数q,使得数列![]() 是3-折叠数列;
是3-折叠数列;
(3)给定常数![]() ,是否存在数列
,是否存在数列![]() 使得对所有
使得对所有![]() ,
,![]() 都是
都是![]() 折叠数列,且
折叠数列,且![]() 的各项中恰有
的各项中恰有![]() 个不同的值,证明你的结论.
个不同的值,证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的侧棱
的侧棱![]() 与四棱锥
与四棱锥![]() 的侧棱
的侧棱![]() 都与底面
都与底面![]() 垂直,
垂直,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
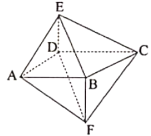
(1)证明:![]() 平面
平面![]() ;
;
(2)在棱![]() 上是否存在点M,使平面
上是否存在点M,使平面![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ?如果存在,指出M点的位置;如果不存在,请说明理由.
?如果存在,指出M点的位置;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com