
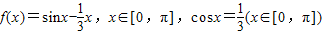 ,那么下面结论正确的是( )
,那么下面结论正确的是( ) x可求其导数f′(x)=cosx-
x可求其导数f′(x)=cosx- ,又余弦函数在[0,π]上单调递减,判断导数在[x,π]上的正负,再根据导数跟单调性的关系判断函数的单调性.
,又余弦函数在[0,π]上单调递减,判断导数在[x,π]上的正负,再根据导数跟单调性的关系判断函数的单调性. x
x
 ,x∈[0,π]
,x∈[0,π]
 <0
<0  x在[x,π]上是减函数.
x在[x,π]上是减函数.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2010-2011学年浙江省嘉兴一中高二(下)3月月考数学试卷(文科)(解析版) 题型:选择题
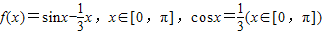 ,那么下面结论正确的是( )
,那么下面结论正确的是( )查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省莆田一中高二(下)第一学段考试数学试卷(选修2-1、2-2)(解析版) 题型:选择题
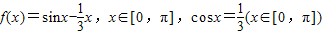 ,那么下面结论正确的是( )
,那么下面结论正确的是( )查看答案和解析>>
科目:高中数学 来源:2010-2011学年北京市海淀区高三(上)期末数学试卷(文科)(解析版) 题型:选择题
 ,那么下面结论正确的是( )
,那么下面结论正确的是( )查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省广州市番禺区仲元中学高三(下)2月月考数学试卷(文科)(解析版) 题型:选择题
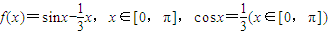 ,那么下面结论正确的是( )
,那么下面结论正确的是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com