
【题目】已知抛物线![]() 与圆
与圆![]() 相交于
相交于![]() ,
,![]() 两点,且点
两点,且点![]() 的横坐标为
的横坐标为![]() .
.![]() 是抛物线
是抛物线![]() 的焦点,过焦点的直线
的焦点,过焦点的直线![]() 与抛物线
与抛物线![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() .
.
(1)求抛物线![]() 的方程.
的方程.
(2)过点![]() ,
,![]() 作抛物线
作抛物线![]() 的切线
的切线![]() ,
,![]() ,
,![]() 是
是![]() ,
,![]() 的交点,求证:点
的交点,求证:点![]() 在定直线上.
在定直线上.
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为
中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为![]() ,曲线C的极坐标方程为
,曲线C的极坐标方程为![]() .
.
(Ⅰ)求直线l和曲线C的直角坐标方程;
(Ⅱ)点M为曲线C上一点,求M到直线l的最小距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年,河南省郑州市的房价依旧是郑州市民关心的话题.总体来说,二手房房价有所下降,相比二手房而言,新房市场依然强劲,价格持续升高.已知销售人员主要靠售房提成领取工资.现统计郑州市某新房销售人员一年的工资情况的结果如图所示,若近几年来该销售人员每年的工资总体情况基本稳定,则下列说法正确的是( )

A.月工资增长率最高的为8月份
B.该销售人员一年有6个月的工资超过4000元
C.由此图可以估计,该销售人员2020年6,7,8月的平均工资将会超过5000元
D.该销售人员这一年中的最低月工资为1900元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,若
时,若![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若定义在![]() 上奇函数
上奇函数![]() 满足
满足![]() ,且当
,且当![]() 时,
时,![]() ,求
,求![]() 在
在![]() 上的解析式;
上的解析式;
(3)对于(2)中的![]() ,若关于
,若关于![]() 的不等式
的不等式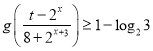 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若双曲线![]() 的实轴长为6,焦距为10,右焦点为
的实轴长为6,焦距为10,右焦点为![]() ,则下列结论正确的是( )
,则下列结论正确的是( )
A.![]() 的渐近线上的点到
的渐近线上的点到![]() 距离的最小值为4B.
距离的最小值为4B.![]() 的离心率为
的离心率为![]()
C.![]() 上的点到
上的点到![]() 距离的最小值为2D.过
距离的最小值为2D.过![]() 的最短的弦长为
的最短的弦长为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 离心率是
离心率是![]() 分别是椭圆
分别是椭圆![]() 的左右焦点,过
的左右焦点,过![]() 作斜率为
作斜率为![]() 的直线
的直线![]() ,交椭圆
,交椭圆![]() 于
于![]() ,
,![]() 两点,且三角形
两点,且三角形![]() 周长
周长![]()
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 分别交
分别交![]() 轴于不同的两点
轴于不同的两点![]() ,
,![]() .如果
.如果![]() 为锐角,求
为锐角,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com