
【题目】袋子里有编号为![]() 的五个球,某位教师从袋中任取两个不同的球. 教师把所取两球编号的和只告诉甲,其乘积只告诉乙,让甲、乙分别推断这两个球的编号.
的五个球,某位教师从袋中任取两个不同的球. 教师把所取两球编号的和只告诉甲,其乘积只告诉乙,让甲、乙分别推断这两个球的编号.
甲说:“我无法确定.”
乙说:“我也无法确定.”
甲听完乙的回答以后,甲又说:“我可以确定了.”
根据以上信息, 你可以推断出抽取的两球中
A. 一定有3号球 B. 一定没有3号球 C. 可能有5号球 D. 可能有6号球
科目:高中数学 来源: 题型:
【题目】在一次购物抽奖活动中,假设某10张券中有一等奖券1张,可获价值50元的奖品;有二等奖券3张,每张可获价值10元的奖品;其余6张没有奖,某顾客从此10张券中任抽2张,求:
(Ⅰ)该顾客中奖的概率;
(Ⅱ)该顾客获得的奖品总价值ξ(元)的概率分布列和期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为 为参数),直线
为参数),直线![]() 和圆
和圆![]() 交于
交于![]() 两点,
两点,![]() 是圆
是圆![]() 上不同于
上不同于![]() 的任意一点.
的任意一点.
(1)求圆心的极坐标;
(2)求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以平面直角坐标系![]() 的原点为极点,
的原点为极点, ![]() 轴正半轴为极轴且取相同的单位长度建立极坐标系.已知点
轴正半轴为极轴且取相同的单位长度建立极坐标系.已知点![]() 的参数方程为
的参数方程为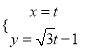 (
(![]() 为参数),点
为参数),点![]() 在曲线
在曲线![]() 上.
上.
(1)求在平面直角坐标系![]() 中点
中点![]() 的轨迹方程和曲线
的轨迹方程和曲线![]() 的普通方程;
的普通方程;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+bx2+cx的导函数图象关于直线x=2对称
(1)求b值;
(2)若f(x)在x=t处取得极小值,记此极小值为g(t),求g(t)的定义域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点 ,椭圆
,椭圆![]() 的左焦点为
的左焦点为![]() ,右焦点为
,右焦点为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上位于
上位于![]() 轴上方的动点,且
轴上方的动点,且![]() ,直线
,直线![]() 与直线
与直线![]() 分别交于
分别交于![]() 两点.
两点.
(1)求椭圆![]() 的方程及线段
的方程及线段![]() 的长度的最小值;
的长度的最小值;
(2)![]() 是椭圆
是椭圆![]() 上一点,当线段
上一点,当线段![]() 的长度取得最小值时,求
的长度取得最小值时,求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=lnx﹣ax+ ![]() ﹣1. (Ⅰ)当a=1时,求曲线f(x)在x=1处的切线方程;
﹣1. (Ⅰ)当a=1时,求曲线f(x)在x=1处的切线方程;
(Ⅱ)当a= ![]() 时,求函数f(x)的单调区间;
时,求函数f(x)的单调区间;
(Ⅲ)在(Ⅱ)的条件下,设函数g(x)=x2﹣2bx﹣ ![]() ,若对于x1∈[1,2],x2∈[0,1],使f(x1)≥g(x2)成立,求实数b的取值范围.
,若对于x1∈[1,2],x2∈[0,1],使f(x1)≥g(x2)成立,求实数b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com