
【题目】已知二次函数![]() 的图象过点
的图象过点![]() ,对任意
,对任意![]() 满足
满足![]() ,且有最小值为
,且有最小值为![]()
![]()
(1)求![]() 的解析式;
的解析式;
(2)求函数![]() 在区间[0,1]上的最小值,其中
在区间[0,1]上的最小值,其中![]() ;
;
(3)在区间[-1,3]上,![]() 的图象恒在函数
的图象恒在函数![]() 的图象上方,试确定实数
的图象上方,试确定实数![]() 的范围.
的范围.
【答案】(1)![]() ;(2)
;(2)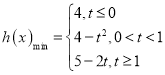 ;(3)
;(3)![]() .
.
【解析】
(1)由题中条件可得函数的对称轴是![]() ,再根据函数最小值为
,再根据函数最小值为![]() 可设出函数方程,再将
可设出函数方程,再将![]() 代入可得解析式;
代入可得解析式;
(2)先得出函数![]() 含未知数
含未知数![]() 的解析式,讨论
的解析式,讨论![]() 的取值范围,在对应范围内分析单调性,得出最小值;
的取值范围,在对应范围内分析单调性,得出最小值;
(3)函数![]() 的图象在
的图象在![]() 的上方,则在
的上方,则在![]() 上
上![]() 恒成立,即
恒成立,即![]() ,即求函数
,即求函数![]() 的最小值,从而求得结果.
的最小值,从而求得结果.
(1)由题知二次函数图象的对称轴为x=![]() ,又最小值是
,又最小值是![]() ,
,
则可设![]() ,又图象过点(0,4),解得a=1.
,又图象过点(0,4),解得a=1.
所以![]() ;
;
(2)h(x)=f(x)-(2t-3)x=x2-2tx+4=(x-t)2+4-t2,其对称轴x=t.
①t≤0时,函数h(x)在[0,1]上单调递增,最小值为h(0)=4;
②当0<t<1时,函数h(x)的最小值为h(t)=4-t2;
③当t≥1时,函数h(x)在0,1]上单调递减,最小值为h(1)=5-2t,
所以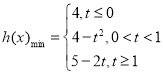 ;
;
(3)由已知:f(x)>2x+m对x∈![]() 恒成立,
恒成立,
∴m<x2-5x+4对x∈![]() 恒成立.
恒成立.
∴m<(x2-5x+4)min (x∈![]() ).
).
∵g(x)=x2-5x+4在x∈![]() 上的最小值为
上的最小值为![]() ,
,
∴m<![]() .
.


科目:高中数学 来源: 题型:
【题目】如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上,D点在AN上,且对角线MN过点C,已知AB=2米,AD=1米.

(1)要使矩形AMPN的面积大于9平方米,则DN的长应在什么范围内?
(2)当DN的长度为多少时,矩形花坛AMPN的面积最小?并求出最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解某省各景区在大众中的熟知度,随机从本省![]() 岁的人群中抽取了
岁的人群中抽取了![]() 人,得到各年龄段人数的频率分布直方图如图所示,现让他们回答问题“该省有哪几个国家
人,得到各年龄段人数的频率分布直方图如图所示,现让他们回答问题“该省有哪几个国家![]() 级旅游景区?”,统计结果如下表所示:
级旅游景区?”,统计结果如下表所示:
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
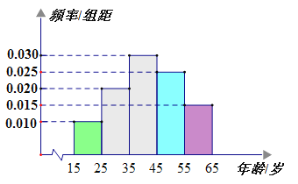
(1)分别求出![]() 的值;
的值;
(2)从第![]() 组回答正确的人中用分层抽样的方法抽取
组回答正确的人中用分层抽样的方法抽取![]() 人,求第
人,求第![]() 组每组抽取的人数;
组每组抽取的人数;
(3)在(2)中抽取的![]() 人中随机抽取
人中随机抽取![]() 人,求所抽取的人中恰好没有年龄段在
人,求所抽取的人中恰好没有年龄段在![]() 的概率
的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() :
:![]() ,已知过点
,已知过点![]() 的直线
的直线![]() 的参数方程为:
的参数方程为: (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 两点.
两点.
(1)写出曲线![]() 和直线
和直线![]() 的普通方程;
的普通方程;
(2)若![]() ,
,![]() ,
,![]() 成等比数列,求
成等比数列,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)假设关于某设备使用年限x(年)和所支出的维修费用y(万元)有如下统计资料:
| 2 | 3 | 4 | 5 | 6 |
| 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知,y对x呈线性相关关系,试求:
(1)回归直线方程;
(2)估计使用年限为10年时,维修费用约是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 为两条不同的直线,
为两条不同的直线,![]() ,
,![]() 为两个不同的平面,给出下列命题:
为两个不同的平面,给出下列命题:
①若![]() ,
,![]() ,则
,则![]() ;
;
②若![]() ,
,![]() ,则
,则![]() ;
;
③若![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
④若![]() ,
,![]() ,则
,则![]() 与
与![]() 所成的角和
所成的角和![]() 与
与![]() 所成的角相等.
所成的角相等.
其中正确命题的序号是( )
A.①②B.①④C.②③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知单位圆O上的两点A,B及单位圆所在平面上的一点P,满足 ![]() =m
=m ![]() +
+ ![]() (m为常数).
(m为常数). 
(1)如图,若四边形OABP为平行四边形,求m的值;
(2)若m=2,求| ![]() |的取值范围.
|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人进行围棋比赛,约定先连胜两局者直接赢得比赛,若赛完5局仍未出现连胜,则判定获胜局数多者赢得比赛,假设每局甲获胜的概率为![]() ,乙获胜的概率为
,乙获胜的概率为![]() ,各局比赛结果相互独立.
,各局比赛结果相互独立.
求甲在4局以内(含4局)赢得比赛的概率;
记![]() 为比赛决出胜负时的总局数,求
为比赛决出胜负时的总局数,求![]() 的分布列和均值(数学期望).
的分布列和均值(数学期望).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com