
【题目】已知椭圆![]() 与抛物线
与抛物线![]() 共焦点
共焦点![]() ,抛物线上的点M到y轴的距离等于
,抛物线上的点M到y轴的距离等于![]() ,且椭圆与抛物线的交点Q满足
,且椭圆与抛物线的交点Q满足![]() .
.
(I)求抛物线的方程和椭圆的方程;
(II)过抛物线上的点![]() 作抛物线的切线
作抛物线的切线![]() 交椭圆于
交椭圆于![]() 、
、![]() 两点,设线段AB的中点为
两点,设线段AB的中点为![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)将抛物线上的点![]() 到
到![]() 轴的距离等于
轴的距离等于![]() 和抛物线的定义相结合,可得
和抛物线的定义相结合,可得![]() ,可得抛物线的方程,已知在椭圆中
,可得抛物线的方程,已知在椭圆中![]() 的值,由
的值,由![]() 可得点Q的坐标,结合椭圆的定义可得椭圆的方程;(2)联立直线与抛物线的方程,结合其有一个交点可得关系式
可得点Q的坐标,结合椭圆的定义可得椭圆的方程;(2)联立直线与抛物线的方程,结合其有一个交点可得关系式![]() ,联立直线与椭圆的方程根据椭圆与直线有2个交点即
,联立直线与椭圆的方程根据椭圆与直线有2个交点即![]() ,得到关于
,得到关于![]() 不等式,解不等式可得
不等式,解不等式可得![]() 的取值范围,由中点坐标公式及韦达定理可得
的取值范围,由中点坐标公式及韦达定理可得![]() ,从而可得其范围.
,从而可得其范围.
试题解析:(1)∵抛物线上的点![]() 到
到![]() 轴的距离等于
轴的距离等于![]() ,
,
∴点M到直线![]() 的距离等于点
的距离等于点![]() 到焦点
到焦点![]() 的距离,
的距离,
得![]() 是抛物线
是抛物线![]() 的准线,即
的准线,即![]() ,
,
解得![]() ,∴抛物线的方程为
,∴抛物线的方程为![]() ;
;
可知椭圆的右焦点![]() ,左焦点
,左焦点![]() ,
,
由![]() 得
得![]() ,又
,又![]() ,解得
,解得![]() ,
,
由椭圆的定义得![]() ,
,
∴![]() ,又
,又![]() ,得
,得![]() ,
,
∴椭圆的方程为![]() .
.
(2)显然![]() ,
, ![]() ,
,
由![]() ,消去
,消去![]() ,得
,得![]() ,
,
由题意知![]() ,得
,得![]() ,
,
由 ,消去
,消去![]() ,得
,得![]() ,
,
其中![]() ,
,
化简得![]() ,
,
又![]() ,得
,得![]() ,解得
,解得![]() ,
,
设![]() ,则
,则![]() <0,
<0,
由![]() ,得
,得![]() ,∴
,∴![]() 的取值范围是
的取值范围是![]() .
.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:
【题目】潍坊文化艺术中心的观光塔是潍坊市的标志性建筑,某班同学准备测量观光塔![]() 的高度
的高度![]() (单位:米),如图所示,垂直放置的标杆
(单位:米),如图所示,垂直放置的标杆![]() 的高度
的高度![]() 米,已知
米,已知![]() ,
, ![]() .
.
(1)该班同学测得![]() 一组数据:
一组数据: ![]() ,请据此算出
,请据此算出![]() 的值;
的值;
(2)该班同学分析若干测得的数据后,发现适当调整标杆到观光塔的距离![]() (单位:米),使
(单位:米),使![]() 与
与![]() 的差较大,可以提高测量精确度,若观光塔高度为136米,问
的差较大,可以提高测量精确度,若观光塔高度为136米,问![]() 为多大时,
为多大时, ![]() 的值最大?
的值最大?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log4(4x+1)+kx(k∈R)是偶函数.
(1)求实数k的值;
(2)设g(x)=log4(a2x+a),若f(x)=g(x)有且只有一个实数解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF∥AB,AB=2,BC=EF=1,AE=![]() ,DE=3,∠BAD=60,G为BC的中点.
,DE=3,∠BAD=60,G为BC的中点.
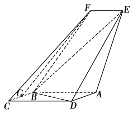
(1)求证:FG![]() 平面BED;
平面BED;
(2)求证:平面BED⊥平面AED;
(3)求直线EF与平面BED所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() 在
在![]() 和
和![]() 处取得极值,且
处取得极值,且![]() ,曲线
,曲线![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直.
垂直.
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)证明关于![]() 的方程
的方程![]() 至多只有两个实数根(其中
至多只有两个实数根(其中![]() 是
是![]() 的导函数,
的导函数, ![]() 是自然对数的底数).
是自然对数的底数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=4x﹣2x+1+3,当x∈[﹣2,1]时,f(x)的最大值为m,最小值为n,
(1)若角α的终边经过点P(m,n),求sinα+cosα的值;
(2)g(x)=mcos(nx+![]() )+n,求g(x)的最大值及自变量x的取值集合.
)+n,求g(x)的最大值及自变量x的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数fk(x)=xk+bx+c(k∈N* , b,c∈R),g(x)=logax(a>0,a≠1).
(1)若b+c=1,且fk(1)=g( ![]() ),求a的值;
),求a的值;
(2)若k=2,记函数fk(x)在[﹣1,1]上的最大值为M,最小值为m,求M﹣m≤4时的b的取值范围;
(3)判断是否存在大于1的实数a,使得对任意x1∈[a,2a],都有x2∈[a,a2]满足等式:g(x1)+g(x2)=p,且满足该等式的常数p的取值唯一?若存在,求出所有符合条件的a的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com