
【题目】已知函数![]() 有两个零点.
有两个零点.
(1)求![]() 的取值范围;
的取值范围;
(2)设![]() ,
,![]() 是
是![]() 的两个零点,证明:
的两个零点,证明:![]() .
.
【答案】(1)![]() 的取值范围为
的取值范围为![]() ;(2)证明见详解.
;(2)证明见详解.
【解析】
(1)求出![]() ,然后分
,然后分![]() 、
、![]() 、
、![]() 、
、![]() 四种情况讨论,每种情况下求出
四种情况讨论,每种情况下求出![]() 的单调性,再结合函数值的符号即可得到答案;
的单调性,再结合函数值的符号即可得到答案;
(2)借助(1)的结论来证明,由单调性可知![]() 等价于
等价于![]() ,即
,即![]() .设
.设![]() ,则
,则![]() .则当
.则当![]() 时,
时,![]() ,而
,而![]() ,故当
,故当![]() 时,
时,![]() .从而
.从而![]() ,故
,故![]() .
.
(1)![]() .
.
①当![]() 时,则
时,则![]() ,
,![]() 只有一个零点.
只有一个零点.
②当![]() 时,则当
时,则当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
又![]() ,
,![]() ,取
,取![]() 满足
满足![]() 且
且![]() ,
,
则![]() ,
,
故![]() 存在两个零点.
存在两个零点.
③当![]() 时,由
时,由![]() 得
得![]() 或
或![]() .
.
若![]() ,则
,则![]() ,故当
,故当![]() 时,
时,![]() ,因此
,因此![]() 在
在![]() 单调递增.
单调递增.
又当![]() 时
时![]() ,所以
,所以![]() 不存在两个零点.
不存在两个零点.
若![]() ,则
,则![]() ,故当
,故当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
因此![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
又当![]() 时,
时,![]() ,所以
,所以![]() 不存在两个零点.
不存在两个零点.
综上,![]() 的取值范围为
的取值范围为![]() .
.
(2)不妨设![]() ,由(1)知
,由(1)知![]() ,
,![]() ,
,
![]() 在
在![]() 单调递减,所以要证
单调递减,所以要证![]() ,即证
,即证![]() ,即证
,即证![]() .
.
由于![]() ,而
,而![]() ,
,
所以![]() .
.
设![]() ,则
,则![]() .
.
所以当![]() 时,
时,![]() ,而
,而![]() ,故当
,故当![]() 时,
时,![]() .
.
从而![]() ,故
,故![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】若![]() =(
=(![]() ,
,![]() ),
),![]() =(
=(![]() ,
,![]() ),设
),设![]() .
.
(1)求函数![]() 在[0,π]上的单调减区间;
在[0,π]上的单调减区间;
(2)在△ABC中,角A,B,C所对的边分别为a,b,c,若![]() ,
,![]() ,求sinB的值.
,求sinB的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知在算法中“![]() ”和“
”和“![]() ”分别表示取商和取余数.为了验证三位数卡普雷卡尔“数字黑洞”(即输入一个无重复数字的三位数,经过如图的有限次的重排求差计算,结果都为495).小明输入
”分别表示取商和取余数.为了验证三位数卡普雷卡尔“数字黑洞”(即输入一个无重复数字的三位数,经过如图的有限次的重排求差计算,结果都为495).小明输入![]() ,则输出的
,则输出的![]() ( )
( )![]()

A.3B.4C.5D.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为
的焦距为![]() ,且过点
,且过点![]() .
.
(1)求C的方程;
(2)若直线l与C有且只有一个公共点,l与圆x2+y2=6交于A,B两点,直线OA,OB的斜率分别记为k1,k2.试判断k1k2是否为定值,若是,求出该定值;否则,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“割圆术”是刘徽最突出的数学成就之一,他在《九章算术注》中提出割圆术,并作为计算圆的周长,面积已经圆周率的基础,刘徽把圆内接正多边形的面积一直算到了正3072边形,并由此而求得了圆周率为3.1415和3.1416这两个近似数值,这个结果是当时世界上圆周率计算的最精确数据.如图,当分割到圆内接正六边形时,某同学利用计算机随机模拟法向圆内随机投掷点,计算得出该点落在正六边形内的频率为0.8269,那么通过该实验计算出来的圆周率近似值为(参考数据:![]() )
)

A. 3.1419B. 3.1417C. 3.1415D. 3.1413
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥PABCD中,PA⊥底面ABCD,AD∥BC,AB=AC=AD=3,PA=BC=4.
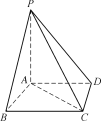
(1)求异面直线PB与CD所成角的余弦值;
(2)求平面PAD与平面PBC所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的有( )
①用相关指数![]() 来刻画回归效果,
来刻画回归效果,![]() 越小,说明模型的拟合效果越好;
越小,说明模型的拟合效果越好;
②若一组数据8,12,x,11,9的平均数是10,则其方差是2;
③回归直线一定过样本点的中心(![]() );
);
④若相关系数![]() ,则两个变量之间线性关系性强.
,则两个变量之间线性关系性强.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 已知函数f(x)=|x+a|+|x-2|.
(1)当a=-3时,求不等式f(x)≥3的解集;
(2)若f(x)≤|x-4|的解集包含[1,2],求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com