
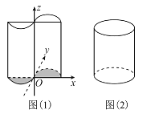
【题目】我国古代数学家祖暅提出原理:“幂势既同,则积不容异”.其中“幂”是截面积,“势”是几何体的高.原理的意思是:夹在两个平行平面间的两个几何体,被任一平行于这两个平行平面的平面所截,若所截的两个截面的面积恒相等,则这两个几何体的体积相等.如图(1),函数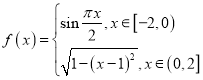 的图象与x轴围成一个封闭区域A(阴影部分),将区域A(阴影部分)沿z轴的正方向上移6个单位,得到一几何体.现有一个与之等高的底面为椭圆的柱体如图(2)所示,其底面积与区域A(阴影部分)的面积相等,则此柱体的体积为______.
的图象与x轴围成一个封闭区域A(阴影部分),将区域A(阴影部分)沿z轴的正方向上移6个单位,得到一几何体.现有一个与之等高的底面为椭圆的柱体如图(2)所示,其底面积与区域A(阴影部分)的面积相等,则此柱体的体积为______.
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:
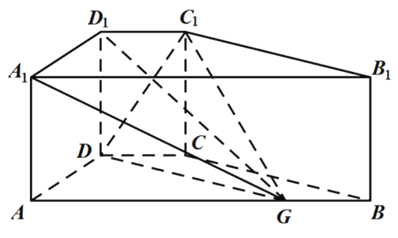
【题目】如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为梯形,AB//CD,∠BAD=60°,CD=1,AD=2,AB=4,点G在线段AB上,AG=3GB,AA1=1
(1)证明:D1G/平面BB1C1C,
(2)求二面角A1-D1G-A的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD-A1B1C1D1中,底面四边形ABCD为菱形,A1A=AB=2,∠ABC=![]() ,E,F分别是BC,A1C的中点.
,E,F分别是BC,A1C的中点.
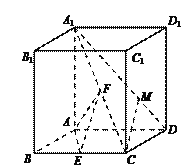
(1)求异面直线EF,AD所成角的余弦值;
(2)点M在线段A1D上, ![]() .若CM∥平面AEF,求实数λ的值.
.若CM∥平面AEF,求实数λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() 与
与![]() 满足
满足![]() ,
,![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() 项和(
项和(![]() ).
).
(1)设数列![]() 是首项和公比都为
是首项和公比都为![]() 的等比数列,且数列
的等比数列,且数列![]() 也是等比数列,求
也是等比数列,求![]() 的值;
的值;
(2)设![]() ,若
,若![]() 且
且![]() 对
对![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)设![]() ,
,![]() ,
,![]() (
(![]() ,
,![]() ),若存在整数
),若存在整数![]() ,
,![]() ,且
,且![]() ,使得
,使得![]() 成立,求
成立,求![]() 的所有可能值.
的所有可能值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】蔬菜批发市场销售某种蔬菜,在一个销售周期内,每售出1吨该蔬菜获利500元,未售出的蔬菜低价处理,每吨亏损100元.统计该蔬菜以往100个销售周期的市场需求量,绘制下图所示频率分布直方图.
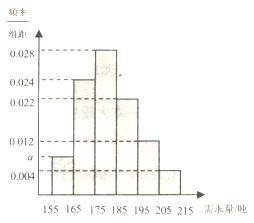
(Ⅰ)求![]() 的值,并求100个销售周期的平均市场需求量(以各组的区间中点值代表该组的数值);
的值,并求100个销售周期的平均市场需求量(以各组的区间中点值代表该组的数值);
(Ⅱ)若经销商在下个销售周期购进了190吨该蔬菜,设![]() 为该销售周期的利润(单位:元),
为该销售周期的利润(单位:元),![]() 为该销售周期的市场需求量(单位:吨).求
为该销售周期的市场需求量(单位:吨).求![]() 与
与![]() 的函数解析式,并估计销售的利润不少于86000元的概率.
的函数解析式,并估计销售的利润不少于86000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高尔顿板是英国生物统计学家高尔顿设计用来研究随机现象的模型,在一块木板上钉着若干排相互平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,前面挡有一块玻璃,让一个小球从高尔顿板上方的通道口落下,小球在下落的过程中与层层小木块碰撞,且等可能向左或向右滚下,最后掉入高尔顿板下方的某一球槽内.如图所示的小木块中,上面7层为高尔顿板,最下面一层为改造的高尔顿板,小球从通道口落下,第一次与第2层中间的小木块碰撞,以![]() 的概率向左或向右滚下,依次经过6次与小木块碰撞,最后掉入编号为1,2…,7的球槽内.例如小球要掉入3号球槽,则在前5次碰撞中有2次向右3次向左滚到第6层的第3个空隙处,再以
的概率向左或向右滚下,依次经过6次与小木块碰撞,最后掉入编号为1,2…,7的球槽内.例如小球要掉入3号球槽,则在前5次碰撞中有2次向右3次向左滚到第6层的第3个空隙处,再以![]() 的概率向左滚下,或在前5次碰撞中有1次向右4次向左滚到第6层的第2个空隙处,再以
的概率向左滚下,或在前5次碰撞中有1次向右4次向左滚到第6层的第2个空隙处,再以![]() 的概率向右滚下.
的概率向右滚下.

(1)若进行一次高尔顿板试验,求小球落入第7层第6个空隙处的概率;
(2)小明同学在研究了高尔顿板后,利用该图中的高尔顿板来到社团文化节上进行盈利性“抽奖”活动,8元可以玩一次高尔顿板游戏,小球掉入X号球槽得到的奖金为![]() 元,其中
元,其中![]() .
.
(i)求X的分布列:
(ii)高尔顿板游戏火爆进行,很多同学参加了游戏,你觉得小明同学能盈利吗?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的右焦点为F,左顶点为A,离心率
)的右焦点为F,左顶点为A,离心率![]() ,且经过圆O:
,且经过圆O:![]() 的圆心.过点F作不与坐标轴重合的直线
的圆心.过点F作不与坐标轴重合的直线![]() 和该椭圆交于MN两点,且直线
和该椭圆交于MN两点,且直线![]()
![]() 分别与直线
分别与直线![]() 交于PQ两点.
交于PQ两点.
(1)求椭圆的方程;
(2)证明:![]() 为直角三角形.
为直角三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合![]() 表示具有下列性质的函数
表示具有下列性质的函数![]() 的集合:①
的集合:①![]() 的定义域为
的定义域为![]() ;②对任意
;②对任意![]() ,都有
,都有![]()
(1)若函数![]() ,证明
,证明![]() 是奇函数;并当
是奇函数;并当![]() ,
,![]() ,求
,求![]() ,
,![]() 的值;
的值;
(2)设函数![]() (a为常数)是奇函数,判断
(a为常数)是奇函数,判断![]() 是否属于
是否属于![]() ,并说明理由;
,并说明理由;
(3)在(2)的条件下,若 ,讨论函数
,讨论函数![]() 的零点个数.
的零点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由郭帆执导吴京主演的电影《流浪地球》于2019年2月5日起在中国内地上映,影片引发了观影热潮,预计《流浪地球》票房收入47亿人民币,超过《红海行动》成为中国影史票房亚军,仅次于《战狼2》.某电影院为了解该影院观看《流浪地球》的观众的年龄构成情况,随机抽取了40名观众,将他们的年龄分成7段:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
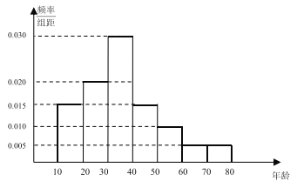
(1)试求这40名观众年龄的平均数、中位数、众数;
(2)(i)若从样本中年龄在50岁以上的观众中任取3名赠送VIP贵宾观影卡,求这3名观众至少有1人年龄不低于70岁的概率;
(ii)该电影院决定采用抽奖方式来提升观影人数,将《流浪地球》电影票票价提高20元,并允许购买电影票的观众抽奖3次,中奖1次、2次、3次分别奖现金![]() 元、
元、![]() 元,
元,![]() 元.设观众每次中奖的概率均为
元.设观众每次中奖的概率均为![]() ,若要使抽奖方案对电影院有利,则
,若要使抽奖方案对电影院有利,则![]() 最高可定为多少元?(结果精确到个位)
最高可定为多少元?(结果精确到个位)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com