
| x | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
科目:高中数学 来源:不详 题型:解答题
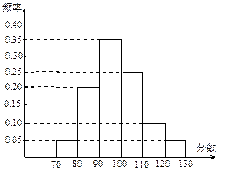
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
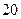 人,得到如下数据:
人,得到如下数据:| 序号 | 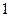 | 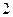 | 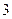 | 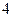 | 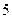 | 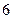 | 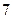 | 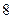 | 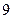 |  |
身高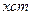 | 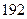 | 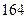 | 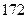 | 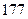 | 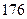 | 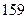 | 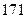 | 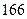 | 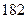 | 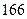 |
脚长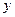 (码) (码) | 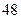 | 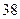 | 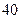 | 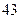 | 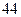 | 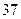 | 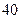 | 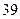 | 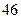 |  |
| 序号 |  |  |  |  | 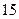 | 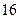 | 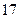 | 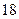 | 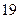 | 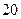 |
身高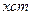 | 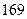 | 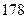 | 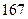 | 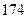 | 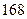 | 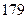 | 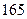 |  | 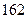 |  |
脚长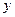 (码) (码) | 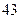 |  | 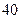 | 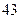 | 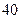 | 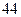 | 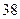 | 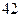 | 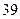 |  |
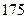 厘米”的为“高个”,“身高小于等于
厘米”的为“高个”,“身高小于等于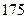 厘米”的为“非高个”;“脚长大于
厘米”的为“非高个”;“脚长大于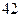 码”的为“大脚”,“脚长小于等于
码”的为“大脚”,“脚长小于等于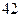 码”的为“非大脚”.
码”的为“非大脚”.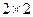 列联表:
列联表: | | 高 个 | 非高个 | 合 计 |
| 大 脚 | | | |
| 非大脚 | | 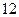 | |
| 合 计 | | | 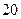 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
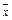 ,方差为S2,则3x1+5、3x2+5、…、3xn+5 的平均值和方差分别为( )
,方差为S2,则3x1+5、3x2+5、…、3xn+5 的平均值和方差分别为( )A.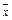 和S2 和S2 | B.3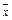 +5和9S2 +5和9S2 | C.3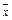 +5和S2 +5和S2 | D.3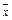 +5和9S2+30S+25 +5和9S2+30S+25 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
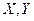 两变量的线性相关性做实验,并用回归分析方法分别求得相关系数
两变量的线性相关性做实验,并用回归分析方法分别求得相关系数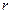 与残差平方和
与残差平方和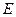 如下表:
如下表:| | 甲 | 乙 | 丙 | 丁 |
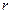 | 0.82 | 0.78 | 0.69 | 0.85 |
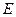 | 106 | 115 | 124 | 103 |
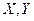 两变量具有更强的线性相关性?( )
两变量具有更强的线性相关性?( )| A.甲 | B.乙 | C.丙 | D.丁 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com