
【题目】广东省的生产总值已经连续30年位居全国第一位,如表是广东省从2012年至2018年7年的生产总值以人民币(单位:万亿元)计算的数据:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
广东省生产总值y(单位:万亿元) | 5.71 | 6.25 | 6.78 | 7.28 | 8.09 | 8.97 | 9.73 |
(1)从表中数据可认为x和y的线性相关性较强,求出以x为解释变量、y为预报变量的线性回归方程(系数精确到0.01);
(2)广东省2018年人口约为1.13亿,德国2018年人口约为0.83亿.从人口数量比较看,广东省比德国人口多,但德国2018年的生产总值为4.00万亿美元,以(1)的结论为依据,预测广东省在哪年的生产总值能超过德国在2018年的生产总值?
参考数据:![]() yi=52.81,
yi=52.81,![]() xiyi=230.05,
xiyi=230.05,![]() yi2=411.2153,
yi2=411.2153,![]() xi2=140.
xi2=140.
货币兑换:1美元≈7.03元人民币
参考公式:回归方程![]() x
x![]() 中斜率
中斜率![]() 和截距
和截距![]() 的最小二乘估计公式分别为:
的最小二乘估计公式分别为: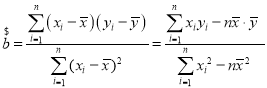 ,
,![]() .
.
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】为了坚决打赢新冠状病毒的攻坚战,阻击战,某小区对小区内的![]() 名居民进行模排,各年龄段男、女生人数如下表.已知在小区的居民中随机抽取
名居民进行模排,各年龄段男、女生人数如下表.已知在小区的居民中随机抽取![]() 名,抽到
名,抽到![]() 岁~
岁~![]() 岁女居民的概率是
岁女居民的概率是![]() .现用分层抽样的方法在全小区抽取
.现用分层抽样的方法在全小区抽取![]() 名居民,则应在
名居民,则应在![]() 岁以上抽取的女居民人数为( )
岁以上抽取的女居民人数为( )
|
|
| |
女生 |
|
|
|
男生 |
|
|
|
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ax+a,a∈R.
(1)求f(x)的单调区间;
(2)当x≥1时,恒有g(x)=(x+1)f(x)﹣lnx≤0恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着甜品的不断创新,现在的甜品无论是造型还是口感都十分诱人,有颜值、有口味、有趣味的产品更容易得到甜品爱好者的喜欢,创新已经成为烘焙作品的衡量标准.某“网红”甜品店生产有几种甜品,由于口味独特,受到越来越多人的喜爱,好多外地的游客专门到该甜品店来品尝“打卡”,已知该甜品店同一种甜品售价相同,该店为了了解每个种类的甜品销售情况,专门收集了该店这个月里五种“网红甜品”的销售情况,统计后得如下表格:
甜品种类 | A甜品 | B甜品 | C甜品 | D甜品 | E甜品 |
销售总额(万元) | 10 | 5 | 20 | 20 | 12 |
销售额(千份) | 5 | 2 | 10 | 5 | 8 |
利润率 | 0.4 | 0.2 | 0.15 | 0.25 | 0.2 |
(利润率是指:一份甜品的销售价格减去成本得到的利润与该甜品的销售价格的比值.)
(1)从该甜品店本月卖出的甜品中随机选一份,求这份甜品的利润率高于0.2的概率;
(2)从该甜品店的五种“网红甜品”中随机选取2种不同的甜品,求这两种甜品的单价相同的概率;
(3)假设每类甜品利润率不变,销售一份A甜品获利![]() 元,销售一份B甜品获利
元,销售一份B甜品获利![]() 元,…,销售一份E甜品获利
元,…,销售一份E甜品获利![]() 元,依据上表统计数据,随机销售一份甜品获利的期望为
元,依据上表统计数据,随机销售一份甜品获利的期望为![]() ,设
,设![]() ,试判断
,试判断![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),曲线
为参数),曲线![]() ,以坐标原点
,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的极坐标方程;
的极坐标方程;
(2)若射线![]() 与曲线
与曲线![]() ,
,![]() 分别交于
分别交于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD-A1B1C1D1中,AD//平面BCC1B1,AD⊥DB.求证:

(1)BC//平面ADD1A1;
(2)平面BCC1B1⊥平面BDD1B1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大城市一家餐饮企业为了了解外卖情况,统计了某个送外卖小哥某天从9:00到21:00这个时间段送的50单外卖.以2小时为一时间段将时间分成六段,各时间段内外卖小哥平均每单的收入情况如下表,各时间段内送外卖的单数的频率分布直方图如下图.
时间区间 |
|
|
|
|
|
|
每单收入(元) | 6 | 5.5 | 6 | 6.4 | 5.5 | 6.5 |
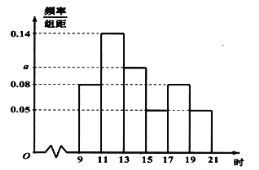
(Ⅰ)求频率分布直方图中![]() 的值,并求这个外卖小哥送这50单获得的收入;
的值,并求这个外卖小哥送这50单获得的收入;
(Ⅱ)在这个外卖小哥送出的50单外卖中男性订了25单,且男性订的外卖中有20单带饮品,女性订的外卖中有10单带饮品,请完成下面的![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为“带饮品和男女性别有关”?
的把握认为“带饮品和男女性别有关”?
带饮品 | 不带饮品 | 总计 | |
男 | |||
女 | |||
总计 |
附:![]()
| 0.050 | 0.010 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com